
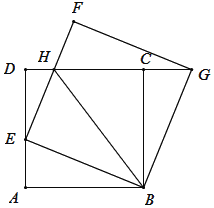
【题目】如图,正方形ABCD的边长为2,点E是AD边上的动点,从点A开始沿AD向D运动.以BE为边,在BE的上方作正方形BEFG,EF交DC于点H,连接CG、BH.请探究:
(1)线段AE与CG是否相等?请说明理由.
(2)若设AE=x,DH=y,当x取何值时,y最大?最大值是多少?
(3)当点E运动到AD的何位置时,△BEH∽△BAE?
【答案】(1)AE=CG,见解析;(2)当x=1时,y有最大值,为![]() ;(3)当E点是AD的中点时,△BEH∽△BAE,见解析.
;(3)当E点是AD的中点时,△BEH∽△BAE,见解析.
【解析】
(1)由正方形的性质可得AB=BC,BE=BG,∠ABC=∠EBG=90°,由“SAS”可证△ABE≌△CBG,可得AE=CG;
(2)由正方形的性质可得∠A=∠D=∠FEB=90°,由余角的性质可得∠ABE=∠DEH,可得△ABE∽△DEH,可得![]() ,由二次函数的性质可求最大值;
,由二次函数的性质可求最大值;
(3)当E点是AD的中点时,可得AE=1,DH=![]() ,可得
,可得![]() ,且∠A=∠FEB=90°,即可证△BEH∽△BAE.
,且∠A=∠FEB=90°,即可证△BEH∽△BAE.
(1)AE=CG,理由如下:
∵四边形ABCD,四边形BEFG是正方形,
∴AB=BC,BE=BG,∠ABC=∠EBG=90°,
∴∠ABE=∠CBG,且AB=BC,BE=BG,
∴△ABE≌△CBG(SAS),
∴AE=CG;
(2)∵四边形ABCD,四边形BEFG是正方形,
∴∠A=∠D=∠FEB=90°,
∴∠AEB+∠ABE=90°,∠AEB+∠DEH=90°,
∴∠ABE=∠DEH,
又∵∠A=∠D,
∴△ABE∽△DEH,
∴![]() ,
,
∴![]()
∴![]() =
=![]() ,
,
∴当x=1时,y有最大值为![]() ;
;
(3)当E点是AD的中点时,△BEH∽△BAE,
理由如下:
∵E是AD中点,
∴AE=1,
∴![]()
又∵△ABE∽△DEH,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,且∠DAB=∠FEB=90°,
,且∠DAB=∠FEB=90°,
∴△BEH∽△BAE.


科目:初中数学 来源: 题型:
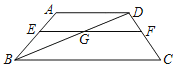
【题目】如图,在梯形ABCD中,点E,F分别在边AB,CD上,AD∥EF∥BC,EF与BD交于点G,AD=5,BC=10,![]() =
=![]() .
.
(1)求EF的长;
(2)设![]() =
=![]() ,
,![]() =
=![]() ,那么
,那么![]() = ,
= ,![]() = .(用向量
= .(用向量![]() 、
、![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
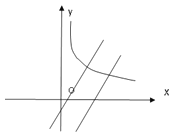
【题目】平面直角坐标系中,函数![]() (x>0),y=x-1,y=x-4的图象如图所示,p(a , b)是直线
(x>0),y=x-1,y=x-4的图象如图所示,p(a , b)是直线![]() 上一动点,且在第一象限.过P作PM∥x轴交直线
上一动点,且在第一象限.过P作PM∥x轴交直线![]() 于M,过P作PN∥y轴交曲线
于M,过P作PN∥y轴交曲线![]() 于N.
于N.
(1)当PM=PN时,求P点坐标
(2)当PM > PN时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦放假期间,小明和小华准备到西安的大雁塔(记为A)、白鹿原(记为B)、兴庆公园(记为C)、秦岭国家植物园(记为D)中的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同.
(1)求小明选择去白鹿原游玩的概率;
(2)用树状图或列表的方法求小明和小华都选择去秦岭国家植物园游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t.
⑴用含t的代数式表示:AP= ,AQ= .
⑵当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
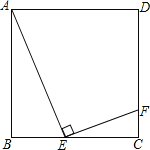
【题目】如图,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.设BE=x,CF=y.
(1)写出y与x的函数关系式.
(2)CF的长可能等于![]() 吗?请说明理由.
吗?请说明理由.
(3)点E在什么位置时,CF的长为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
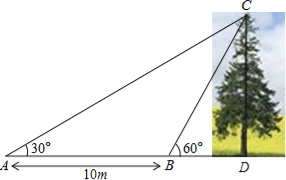
【题目】如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把函数C1:y=ax2﹣2ax﹣3a(a≠0)的图象绕点P(m,0)旋转180°,得到新函数C2的图象,我们称C2是C1关于点P的相关函数.C2的图象的对称轴与x轴交点坐标为(t,0).
(1)填空:t的值为 (用含m的代数式表示)
(2)若a=﹣1,当![]() ≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
≤x≤t时,函数C1的最大值为y1,最小值为y2,且y1﹣y2=1,求C2的解析式;
(3)当m=0时,C2的图象与x轴相交于A,B两点(点A在点B的右侧).与y轴相交于点D.把线段AD原点O逆时针旋转90°,得到它的对应线段A′D′,若线A′D′与C2的图象有公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生某科目学期总评成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果学期总评成绩80分以上(含80分),则评定为“优秀”,下表是小张和小王两位同学的成绩记录:
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 | _______ |
若按完成作业、单元检测、期末考试三项成绩按1:2:7的权重来确定学期总评成绩.
(1)请计算小张的学期总评成绩为多少分?
(2)小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com