
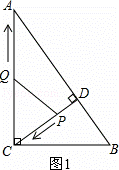
��ͼ����Rt��ABC�У���ACB=90�㣬AC=8��BC=6��CD��AB�ڵ�D����P�ӵ�D���������߶�DC���C�˶�����Q�ӵ�C���������߶�CA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ�����P�˶���Cʱ�����㶼ֹͣ�����˶�ʱ��Ϊt�룮
��1�����߶�CD�ij���
��2�����CPQ�����ΪS����S��t֮��ĺ�����ϵʽ����ȷ�����˶��������Ƿ����ijһʱ��t��ʹ��S��CPQ��S��ABC=9��100�������ڣ����t��ֵ���������ڣ�˵�����ɣ�
��3����tΪ��ֵʱ����CPQΪ���������Σ�
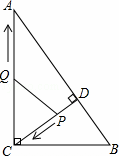


�⣺��1����ͼ1��
�ߡ�ACB=90�㣬AC=8��BC=6��
��AB=10��
��CD��AB��
��S��ABC=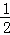 BC•AC=
BC•AC=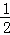 AB•CD��
AB•CD��
��CD=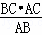 =
=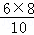 =4.8��
=4.8��
���߶�CD�ij�Ϊ4.8��
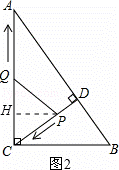
��2���ٹ���P��PH��AC������ΪH����ͼ2��ʾ��
�����֪DP=t��CQ=t��
��CP=4.8��t��
�ߡ�ACB=��CDB=90�㣬
���HCP=90�㩁��DCB=��B��
��PH��AC��
���CHP=90�㣮
���CHP=��ACB��
���CHP�ס�BCA��
��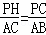 ��
��
��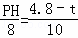 ��
��
��PH=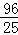 ��
��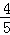 t��
t��
��S��CPQ=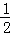 CQ•PH=
CQ•PH=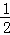 t��
t��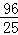 ��
��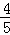 t��=��
t��=��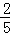 t2+
t2+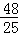 t��
t��
�ڴ���ijһʱ��t��ʹ��S��CPQ��S��ABC=9��100��
��S��ABC=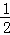 ��6��8=24��
��6��8=24��
��S��CPQ��S��ABC=9��100��
�ࣨ��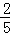 t2+
t2+
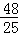 t����24=9��100��
t����24=9��100��
�����ã�5t2��24t+27=0��
����5t��9����t��3��=0��
��ã�t=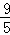 ��t=3��
��t=3��
��0��t��4.8��
�൱t=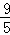 ���t=3��ʱ��S��CPQ��S��ABC=9��100��
���t=3��ʱ��S��CPQ��S��ABC=9��100��
��3������CQ=CP����ͼ1��
��t=4.8��t��
��ã�t=2.4��
����PQ=PC����ͼ2��ʾ��
��PQ=PC��PH��QC��
��QH=CH=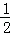 QC=
QC=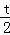 ��
��
�ߡ�CHP�ס�BCA��
��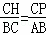 ��
��
��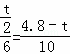 ��
��
��ã�t=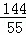 ��
��
����QC=QP��
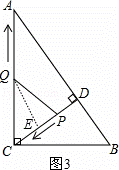
����Q��QE��CP������ΪE����ͼ3��ʾ��
ͬ���ɵã�t=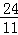 ��
��
������������tΪ2.4���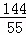 ���
���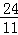 ��ʱ����CPQΪ���������Σ�
��ʱ����CPQΪ���������Σ�




 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��һ��������ֽƬ������ͼ����٣��ڣ������߶������Σ�Ȼ���آ��е�����ȥһ���ǣ�չ����ƽ���ͼ���ǣ�������
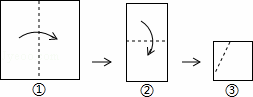
�� A�� B��
B��  C��
C��  D��
D�� 


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
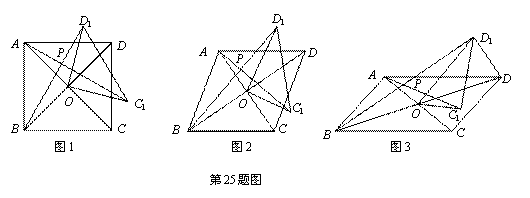
���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O������COD�Ƶ�O����ʱ�뷽����ת�õ���C1OD1����ת��Ϊ����0�㣼����90�㣩������AC1��BD1��AC1��BD1���ڵ�P.
��1����ͼ1�����ı���ABCD��������.
����֤����AOC1�ա�BOD1.
����ֱ��д��AC1 ��BD1��λ�ù�ϵ.
��2����ͼ2�����ı���ABCD�����Σ�AC=5��BD=7����AC1=k BD1.�ж�AC1��BD1��λ�ù�ϵ��˵�����ɣ������k��ֵ.
��3����ͼ3�����ı���ABCD��ƽ���ı��Σ�AC=5��BD=10������DD1����AC1=kBD1.

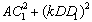 ��ֱ��д��k��ֵ�� ��ֵ.
��ֱ��д��k��ֵ�� ��ֵ.
 |


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڵ�����ABC�У�AB=AC��BC���ϵĸ�AD=6cm����AB�ϵĸ�CE=8cm�����ABC���ܳ��������� cm��
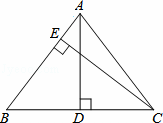


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij��Ϊ����ѧ���������仯�������ȫ�о��꼶ѧ���г�ȡ�˲���ѧ����ͳ����ÿ�������������������Ľ���������������ݴ������Ƴ�����ͳ��ͼ������ͳ��ͼ���£�
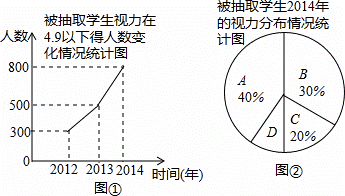
����������⣺
��1��ͼ���С�D��5.2���ϡ����ڵ����ε�Բ�ĽǶ���Ϊ������
��2�����й���ȡ�˶��������꼶ѧ����
��3�������й���10�������꼶ѧ����������Ƹ��о��꼶����5.2���ϵ�ѧ����Լ�ж����ˣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����x�ķ�ʽ����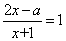 �Ľ�Ϊ����������ĸa��ȡֵ��ΧΪ ( )
�Ľ�Ϊ����������ĸa��ȡֵ��ΧΪ ( )
A��a��-1 B��a>-1 C��a��-1 D��a <-1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij����һ̨�����Ĺ���Ч���൱��һ�����˹���Ч�ʵ�12��������̨��������60�������8������������Щ�������2Сʱ������̨����ÿСʱ������ ���������


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com