
| A. | ①② | B. | ③④ | C. | ②③ | D. | ②④ |
分析 ①通过解方程得到该方程的根,结合“倍根方程”的定义进行判断;
②设x2=2x1,得到x1•x2=2x12=2,得到当x1=1时,x2=2,当x1=-1时,x2=-2,于是得到结论;
③根据“倍根方程”的定义即可得到结论;
④若点(m,n)在反比例函数y=$\frac{4}{x}$的图象上,得到mn=4,然后解方程mx2+5x+n=0即可得到正确的结论;
解答 解:①由x2-2x-8=0,得
(x-4)(x+2)=0,
解得x1=4,x2=-2,
∵x1≠2x2,或x2≠2x1,
∴方程x2-2x-8=0不是倍根方程.
故①错误;
②关于x的方程x2+ax+2=0是倍根方程,
∴设x2=2x1,
∴x1•x2=2x12=2,
∴x1=±1,
当x1=1时,x2=2,
当x1=-1时,x2=-2,
∴x1+x2=-a=±3,
∴a=±3,故②正确;
③关于x的方程ax2-6ax+c=0(a≠0)是倍根方程,
∴x2=2x1,
∵抛物线y=ax2-6ax+c的对称轴是直线x=3,
∴抛物线y=ax2-6ax+c与x轴的交点的坐标是(2,0)和(4,0),
故③正确;
④∵点(m,n)在反比例函数y=$\frac{4}{x}$的图象上,
∴mn=4,
解mx2+5x+n=0得x1=-$\frac{2}{m}$,x2=-$\frac{8}{m}$,
∴x2=4x1,
∴关于x的方程mx2+5x+n=0不是倍根方程;
故选C.
点评 本题考查了反比例函数图象上点的坐标特征,根与系数的关系,正确的理解倍根方程的定义是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
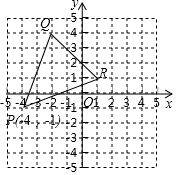 如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )| A. | (-1,-3) | B. | (-2,4) | C. | (-2,-4) | D. | (2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>1 | B. | -3<x<1 | C. | x>-3 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
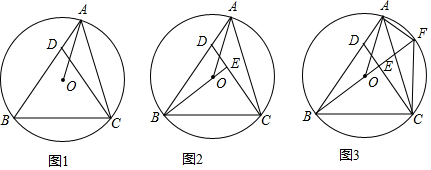
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{4}{3}$ | B. | m≥4 | C. | m<4 | D. | m≤$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.15×106 | B. | 0.115×106 | C. | 11.5×104 | D. | 1.15×105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com