
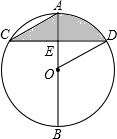
 如图,AB是⊙O的直径,弦CD⊥AB,∠AOD=60°,CD=4$\sqrt{3}$cm.则图中阴影部分的面积S阴影=$\frac{8}{3}$.
如图,AB是⊙O的直径,弦CD⊥AB,∠AOD=60°,CD=4$\sqrt{3}$cm.则图中阴影部分的面积S阴影=$\frac{8}{3}$. 分析 根据垂径定理求得CE=ED=2$\sqrt{3}$,然后通过解直角三角形求得线段OD、OE的长度,最后将相关线段的长度代入S阴影=S扇形ODA-S△DOE+S△AEC.
解答 解:如图∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2$\sqrt{3}$,
∵∠AOD=60°,
∴OE=DE•cot60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,OD=2OE=4,
∴S阴影=S扇形ODA-S△DOE+S△AEC=$\frac{60π×O{D}^{2}}{360}$-$\frac{1}{2}$OE×ED+$\frac{1}{2}$AE•EC=$\frac{8}{3}$π-$\frac{1}{2}$×2×2$\sqrt{3}$+$\frac{1}{2}$×2×2$\sqrt{3}$=$\frac{8}{3}$π.
故答案为$\frac{8}{3}$π.
点评 本题考查了垂径定理、扇形面积的计算,通过解直角三角形得到相关线段的长度是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:
为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级.随机抽取该校部分学生的征文比赛成绩进行统计分析,并绘制了如下的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 占抽查学生总数的百分比 | 30% | 50% | 15% | m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
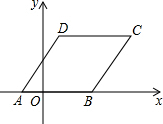 如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )
如图坐标系,四边形ABCD是菱形,顶点A、B在x轴上,AB=5,点C在第一象限,且菱形ABCD的面积为20,A坐标为(-2,0),则顶点C的坐标为( )| A. | (4,3) | B. | (5,4) | C. | (6,4) | D. | (7,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com