
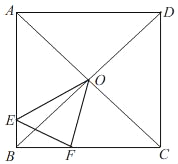
【题目】如图,O为正方形ABCD对角线的交点,E为AB边上一点,F为BC边上一点,△EBF的周长等于BC的长.
(1)若AB=12,BE=3,求EF的长;
(2)求∠EOF的度数;
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.
【答案】(1)5;(2)45°;(3)![]()
【解析】
(1)设BF=x,则FC=12-x,根据△EBF的周长等于BC的长得出EF=9-x,Rt△BEF中利用勾股定理求出x的值即可得;(2)在FC上截取FM=FE,连接OM.首先证明∠EOM=90°,再证明△OFE≌△OFM(SSS)即可解决问题;(3)证明∠FOC=∠AEO,结合∠EAO=∠OCF=45°可证△AOE∽△CFO得![]() ,推出AE=
,推出AE=![]() OC,AO=
OC,AO=![]() CF,由AO=CO,可得AE=
CF,由AO=CO,可得AE=![]() ×
×![]() CF=
CF=![]() CF,进而求解.
CF,进而求解.
(1)设BF=x,则FC=BC﹣BF=12﹣x,
∵BE=3,且BE+BF+EF=BC,
∴EF=9﹣x,
在Rt△BEF中,由BE2+BF2=EF2可得32+x2=(9﹣x)2,
解得:x=4,
则EF=9﹣x=5;
(2)如图,在FC上截取FM=FE,连接OM,
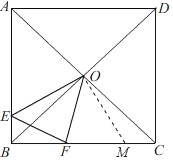
∵C△EBF的周长=BE+EF+BF=BC,则BE+EF+BF=BF+FM+MC,
∴BE=MC,
∵O为正方形中心,
∴OB=OC,∠OBE=∠OCM=45°,
在△OBE和△OCM中,
∵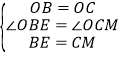 ,
,
∴△OBE≌△OCM,
∴∠EOB=∠MOC,OE=OM,
∴∠EOB+∠BOM=∠MOC+∠BOM,即∠EOM=∠BOC=90°,
在△OFE与△OFM中,
∵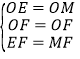 ,
,
∴△OFE≌△OFM(SSS),
∴∠EOF=∠MOF=![]() ∠EOM=45°.
∠EOM=45°.
(3)证明:由(2)可知:∠EOF=45°,
∴∠AOE+∠FOC=135°,
∵∠EAO=45°,
∴∠AOE+∠AEO=135°,
∴∠FOC=∠AEO,
∵∠EAO=∠OCF=45°,
∴△AOE∽△CFO.
∴![]() ,
,
∴AE=![]() OC,AO=
OC,AO=![]() CF,
CF,
∵AO=CO,
∴AE=![]() ×
×![]() CF=
CF=![]() CF,
CF,
∴![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】结论:直角三角形中,![]() 的锐角所对的直角边等于斜边的一半.
的锐角所对的直角边等于斜边的一半.
如图①,我们用几何语言表示如下:
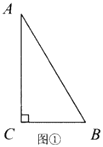
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
你可以利用以上这一结论解决以下问题:
如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
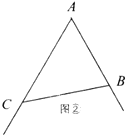
(1)求![]() 的面积;
的面积;
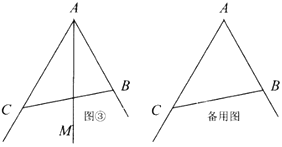
(2)如图③,射线![]() 平分
平分![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着射线
出发,以每秒1个单位的速度沿着射线![]() 的方向运动,过点
的方向运动,过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒,当
秒,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
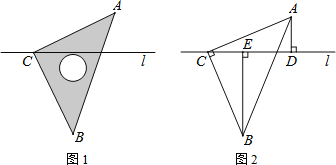
(1)△ACD与△CBE全等吗?说明你的理由.
(2)猜想线段AD、BE、DE之间的关系.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④APAD=CQCB.其中正确的是( )
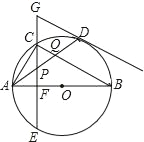
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3000元购进某种干果销售,由于销售状况良好,很快售完.超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果的数量是第一次的2倍还多300千克,如果超市此时按每千克9元的价格出售,当大部分干果售出后,余下的100千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市第二次销售该种干果盈利了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣4ax+c经过点A(0,2),顶点B的纵坐标为3.将直线AB向下平移,与x轴、y轴分别交于点C、D,与抛物线的一个交点为P,若D是线段CP的中点,则点P的坐标为________.
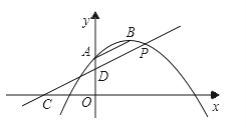
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购买
份),并规定:顾客每购买![]() 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券![]() 元.
元.
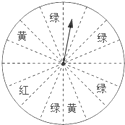
(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费![]() 元,你会选择转转盘还是直接获得购物券?说明理由.
元,你会选择转转盘还是直接获得购物券?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com