列方程解应用题:
(1)在宽20m,长32m的矩形耕地上,修筑同样宽的三条道路.把耕地分成大小相等的六块试验地,要使试验地总面积变为570m2,那么道路的宽应为多少米?
(2)新华商场销售某种冰箱,每台进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的降价应为多少元?
解:(1)
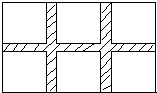
设道路为x米宽,
由题意得:20×32-20x×2-32x+2x
2=570,
整理得:x
2-36x+35=0,
解得:x=1,x=35,
经检验是原方程的解,但是x=35>20,因此不合题意舍去.
答:道路为1m宽.
(2)设每台冰箱的定价应为x元,依题意得(x-2500)(8+
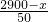
•4)=5000
解方程得x
1=x
2=2750
经检验x
1=x
2=2750符合题意.
答:每台冰箱的定价应为2750元.
分析:(1)试验地的面积=矩形耕地的面积-三条道路的面积+道路重叠部分的两个小正方形的面积.如果设道路宽x,可根据此关系列出方程求出x的值,然后将不合题意的舍去即可.
(2)销售利润=一台冰箱的利润×销售冰箱数量,一台冰箱的利润=售价-进价,降低售价的同时,销售量就会提高,“一减一加”,根据每台的盈利×销售的件数=5000元,即可列方程求解.
点评:此题主要考查了一元二次方程的应用,对于面积问题应熟记各种图形的面积公式.整体面积=各部分面积之和;剩余面积=原面积-截去的面积.

 设道路为x米宽,
设道路为x米宽,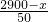 •4)=5000
•4)=5000
