Question

若方程2x²-3x-m=0有两个正根，则整数m为    ．

Answer 1

【答案】分析：因为方程2x²-3x-m=0有两个正根，所以两根之积大于零，而两根的和是，即两根之积是＞0；并且△≥0，即（-3）²-4×2×（-m）≥0解不等式组可得m的值．
解答：解：设方程2x²-3x-m=0的两个根分别为α、β．
∵方程2x²-3x-m=0有两个正根，
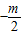
∴αβ=＞0解得m＜0．
又∵方程2x²-3x-m=0有两个根
∴△≥0，即（-3）²-4×2×（-m）≥0，整理得9+8m≥0，解得m≥．
∵m为整数，且0＞m≥，
∴m=-1．
点评：本题综合考查了根与系数的关系与根的判别式，同时考查了不等式组的解法．