
【题目】函数f(x)=ex(﹣x2+2x+a)在区间[a,a+1]上单调递增,则实数a的最大值为 .
【答案】![]()
【解析】解:f(x)=ex(﹣x2+2x+a), f′(x)=ex(﹣x2+a+2),
若f(x)在[a,a+1]上单调递增,
则﹣x2+a+2≥0在[a,a+1]恒成立,
即a+2≥x2在[a,a+1]恒成立,
①a+1<0即a<﹣1时,y=x2在[a,a+1]递减,
y=x2的最大值是y=a2 ,
故a+2≥a2 , 解得:a2﹣a﹣2≤0,解得:﹣1<a<2,不合题意,舍;
②﹣1≤a≤0时,y=x2在[a,0)递减,在(0,a+1]递增,
故y=x2的最大值是a2或(a+1)2 ,
③a>0时,y=x2在[a,a+1]递增,y的最大值是(a+1)2 ,
故a+2≥(a+1)2 , 解得:0<a≤ ![]() ,
,
则实数a的最大值为: ![]() ,
,
综上,a的最大值是 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).


科目:初中数学 来源: 题型:
【题目】已知:如图,正比例函数y=ax的图象与反比例函数y= ![]() 的图象交于点A(3,2)
的图象交于点A(3,2) 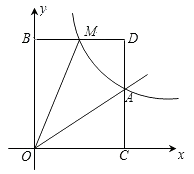
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017赤峰)已知平行四边形ABCD. 
(1)尺规作图:作∠BAD的平分线交直线BC于点E,交DC延长线于点F(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,求证:CE=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.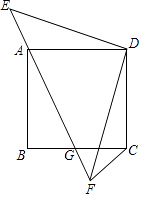
查看答案和解析>>
科目:初中数学 来源: 题型:
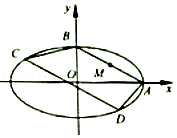
【题目】如图,在平面直角坐标系xoy中,椭圆 ![]() 的右顶点和上顶点分别为点A,B,M是线段AB的中点,且
的右顶点和上顶点分别为点A,B,M是线段AB的中点,且 ![]() ..
.. 
(1)求椭圆的离心率;
(2)若a=2,四边形ABCD内接于椭圆,AB∥CD,记直线AD,BC的斜率分别为k1 , k2 , 求证:k1k2为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1 , S2 , S3三部分,则S1:S2:S3=( ) 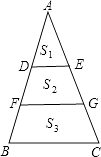
A.1:2:3
B.1:4:9
C.1:3:5
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为( )
A.2cm
B.14cm
C.2cm或14cm
D.10cm或20cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com