
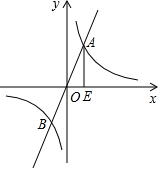
 如图,已知函数y=2x图象和函数y=
如图,已知函数y=2x图象和函数y=| k |
| x |
|
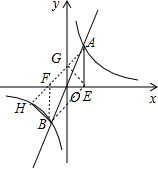 解:设A(t,2t),
解:设A(t,2t),| 1 |
| 2 |
| k |
| x |
|
|
|
|
|
| 42+(2+2)2 |
| 2 |
| 42+(2+2)2 |
| 2 |


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
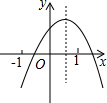 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=0.5,判断点(a+b+c,abc)在第( )象限.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=0.5,判断点(a+b+c,abc)在第( )象限.| A、一 | B、二 | C、三 | D、四 |
查看答案和解析>>
科目:初中数学 来源: 题型:
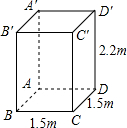 小敏家住在20层的高楼上,一天,她与妈妈去买竹竿,如果电梯的长、宽、高分别是1.5m、1.5m、2.2m,那么,能放入电梯的竹竿最长大约是多少米?你能帮助小敏解决这个问题吗?
小敏家住在20层的高楼上,一天,她与妈妈去买竹竿,如果电梯的长、宽、高分别是1.5m、1.5m、2.2m,那么,能放入电梯的竹竿最长大约是多少米?你能帮助小敏解决这个问题吗?查看答案和解析>>
科目:初中数学 来源: 题型:
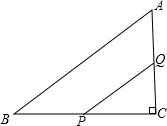 如图,在△ABC中,∠C=90°,BC=8cm,tanB=
如图,在△ABC中,∠C=90°,BC=8cm,tanB=| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
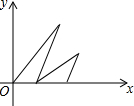 如图,若将图中的五个点的纵坐标保持不变,横坐标分别变成原来的4倍,连接各点所得图案与原图案相比( )
如图,若将图中的五个点的纵坐标保持不变,横坐标分别变成原来的4倍,连接各点所得图案与原图案相比( )| A、相同 | ||
B、横向缩短为原来的
| ||
| C、横向拉长为原来的2倍 | ||
| D、横向拉长为原来的4倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:
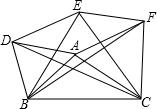 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE、EF判断哪几个三角形与△ABC全等,并证明四边形ADEF是平行四边形.
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE、EF判断哪几个三角形与△ABC全等,并证明四边形ADEF是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com