
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
【答案】
(1)
证明:∵△ABC是等腰三角形,且∠BAC=120°,
∴∠ABD=∠ACB=30°,
∴∠ABD=∠ADE=30°,
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB,
∴△ABD∽△DCE;
(2)
解:如图1,∵AB=AC=2,∠BAC=120°,
过A作AF⊥BC于F,

∴∠AFB=90°,
∵AB=2,∠ABF=30°,
∴AF= ![]() AB=1,
AB=1,
∴BF= ![]() ,
,
∴BC=2BF=2 ![]() ,
,
则DC=2 ![]() ﹣x,EC=2﹣y,
﹣x,EC=2﹣y,
∵△ABD∽△DCE,
∴ ![]() ,
,
∴ ![]() ,
,
化简得:y= ![]() x+2(0<x<2
x+2(0<x<2 ![]() );
);
(3)
解:当AD=DE时,如图2,

由(1)可知:此时△ABD∽△DCE,
则AB=CD,即2=2 ![]() ﹣x,
﹣x,
x=2 ![]() ﹣2,代入y=
﹣2,代入y= ![]() x+2,
x+2,
解得:y=4﹣2 ![]() ,即AE=4﹣2
,即AE=4﹣2 ![]() ,
,
当AE=ED时,如图3,

∠EAD=∠EDA=30°,∠AED=120°,
∴∠DEC=60°,∠EDC=90°,
则ED= ![]() EC,即y=
EC,即y= ![]() (2﹣y),
(2﹣y),
解得:y= ![]() ,即AE=
,即AE= ![]() ,
,
当AD=AE时,
∠AED=∠EDA=30°,∠EAD=120°,
此时点D与点B重合,不符合题意,此情况不存在,
∴当△ADE是等腰三角形时,AE=4﹣2 ![]() 或
或 ![]() .
.
【解析】(1)根据两角相等证明:△ABD∽△DCE;(2)如图1,作高AF,根据直角三角形30°的性质求AF的长,根据勾股定理求BF的长,则可得BC的长,根据(1)中的相似列比例式可得函数关系式,并确定取值;(3)分三种情况进行讨论:①当AD=DE时,如图2,由(1)可知:此时△ABD∽△DCE,则AB=CD,即2=2 ![]() ﹣x;②当AE=ED时,如图3,则ED=
﹣x;②当AE=ED时,如图3,则ED= ![]() EC,即y=
EC,即y= ![]() (2﹣y);③当AD=AE时,∠AED=∠EDA=30°,∠EAD=120°,
(2﹣y);③当AD=AE时,∠AED=∠EDA=30°,∠EAD=120°,
此时点D与点B重合,不符合题意,此情况不存在.
【考点精析】利用函数关系式和等腰三角形的性质对题目进行判断即可得到答案,需要熟知用来表示函数关系的数学式子叫做函数解析式或函数关系式;等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立. 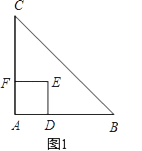
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由. 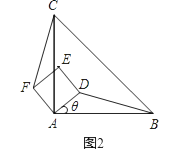
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G. 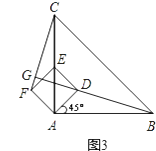
①求证:BD⊥CF;
②当AB=4,AD= ![]() 时,求线段BG的长.
时,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在△ABC中,AO是BC边上的中线,AB与AC的“极化值”就等于AO2﹣BO2的值,可记为AB△AC=AO2﹣BO2 .
(1)在图1中,若∠BAC=90°,AB=8,AC=6,AO是BC边上的中线,则AB△AC= , OC△OA=;
(2)如图2,在△ABC中,AB=AC=4,∠BAC=120°,求AB△AC、BA△BC的值;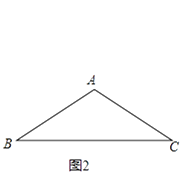
(3)如图3,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON= ![]() AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
AO.已知AB△AC=14,BN△BA=10,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
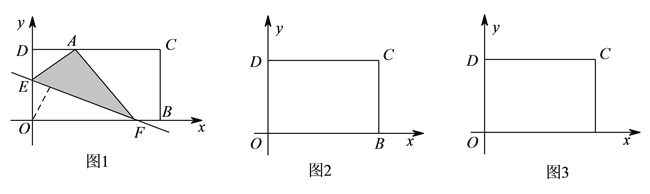
【题目】问题:在平面直角坐标系![]() 中,一张矩形纸片
中,一张矩形纸片![]() 按图
按图![]() 所示放置.已知
所示放置.已知![]() ,
, ![]() ,将这张纸片折叠,使点
,将这张纸片折叠,使点![]() 落在边
落在边![]() 上,记作点
上,记作点![]() ,折痕与边
,折痕与边![]() (含端点).
(含端点).
交于点![]() ,与边
,与边![]() (含端点)或其延长线交于点
(含端点)或其延长线交于点![]() .
.
问题探究:
(![]() )如图
)如图![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,直接写出点
,直接写出点![]() 的坐标________;
的坐标________;
(![]() )将矩形沿直线
)将矩形沿直线![]() 折叠,求点
折叠,求点![]() 的坐标;
的坐标;
问题解决:
(![]() )将矩形沿直线
)将矩形沿直线![]() 折叠,点
折叠,点![]() 在边
在边![]() 上(含端点),求
上(含端点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
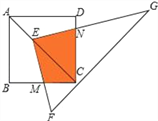
A. ![]() a2 B.
a2 B. ![]() a2 C.
a2 C. ![]() a2 D.
a2 D. ![]() a2
a2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com