
分析 (1)根据题意可以分别求出y1、y2与x之间的函数关系式;
(2)令(1)中两个函数值相等,即可解答本题;
(3)根据(2)中的答案和题意可以求得不同的通话时间,用户如何选择业务;
(4)根据(3)中的结果可以解答本题.
解答 解:(1)由题意可得,
y1与x之间的函数关系式是:y1=50+0.4x,
y2与x之间的函数关系式是:y2=0.6x;
(2)由题意可得,
若y1=y2,则50+0.4x=0.6x,得x=250,
答:一个月内通话250分钟,两种移动通讯费用相同;
(3)由(2)知,
通话250分钟两种移动通讯费用相同,而全球通每分钟付话费0.4元,神州行每分钟付话费0.6元,
∴当通话时间少于250分钟时,选择神州行,当通话250分钟时,另种通讯业务一样,当通话时间多于250分钟时,选择全球通业务;
(4)∵300>250,
∴某人选择全球通业务.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15° | B. | 30° | C. | 30°或60° | D. | 30°或150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
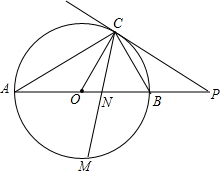 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com