
【题目】如图,直线y=x+b与双曲线y=![]() (k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.
(k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.
(1)求直线和双曲线的解析式;
(2)若△BCP的面积等于2,求P点的坐标;
(3)求PA+PC的最短距离.
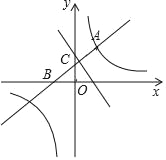
【答案】(1)直线的解析式为y=x+1;(2)P点的坐标为(3,0)或(﹣5,0);(3)![]()
【解析】试题分析:(1)把A(1,2)代入双曲线以及直线y=x+b,分别可得k,b的值;
(2)先根据直线解析式得到BO=CO=1,再根据△BCP的面积等于2,即可得到P的坐标.
(3)作C关于x轴的对称点C′,此时PA+PC最短,最短距离可利用勾股定理求得.
试题解析:解:(1)把A(1,2)代入双曲线y=![]() ,可得:k=2,∴双曲线的解析式为y=
,可得:k=2,∴双曲线的解析式为y=![]() ;
;
把A(1,2)代入直线y=x+b,可得:b=1,∴直线的解析式为y=x+1;
(2)设P点的坐标为(x,0),在y=x+1中,令y=0,则x=﹣1;令x=0,则y=1,∴B(﹣1,0),C(0,1),即BO=1=CO.∵△BCP的面积等于2,∴![]() BP×CO=2,即
BP×CO=2,即![]() |x﹣(﹣1)|×1=2,解得:x=3或﹣5,∴P点的坐标为(3,0)或(﹣5,0).
|x﹣(﹣1)|×1=2,解得:x=3或﹣5,∴P点的坐标为(3,0)或(﹣5,0).
(3)如图,作C关于x轴的对称点C′,则C(0,﹣1).
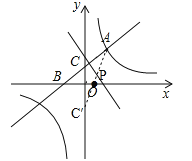
此时PA+PC最短,最短距离是![]() .
.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
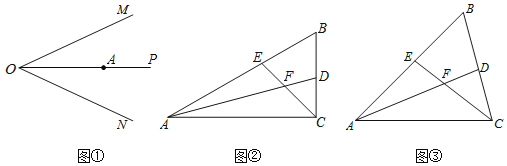
【题目】(1)如图①,OP是∠MON的平分线,点A为OP上一点,请你作一个∠BAC,B、C分别在OM、ON上,且使AO平分∠BAC(保留作图痕迹);
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,△ABC的平分线AD,CE相交于点F,请你判断FE与FD之间的数量关系(可类比(1)中的方法);
(3)如图③,在△ABC中,如果∠ACB≠90°,而(2)中的其他条件不变,请问(2)中所得的结论是否仍然成立?若成立,请证明,若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为
米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为![]() 米,一级台阶高为
米,一级台阶高为![]() 米,如图所示,若此时落在地面上的影长为
米,如图所示,若此时落在地面上的影长为![]() 米,则树高为( )
米,则树高为( )
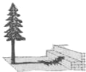
A. 11.5米 B. 11.75米 C. 11.8米 D. 12.25米
查看答案和解析>>
科目:初中数学 来源: 题型:
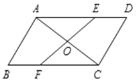
【题目】如图,AC是平行四边形ABCD的一条对角线,过AC中点O的直线分别交 AD,BC 于点 E,F.
(1)求证:四边形AECF是平行四边形;
(2)当 EF 与 AC 满足什么条件时,四边形 AECF 是菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某水果店进行了一次促销活动,一次性购买![]() 种水果的单价
种水果的单价![]() (元)与购买量
(元)与购买量![]() (千克)的函数关系如图.
(千克)的函数关系如图.
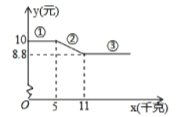
(1)当![]() 时,单价
时,单价![]() 为_______元.
为_______元.
(2)求图中第②段函数图象的解析式,并指出![]() 的取值范围.
的取值范围.
(3)促销活动期间,张老师计划去该店买![]() 种水果10千克,那么张老师共需花费多少钱?
种水果10千克,那么张老师共需花费多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
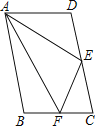
【题目】如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
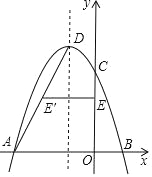
【题目】如图,二次函数y=﹣![]() +mx+4﹣m的图象与x轴交于A、B两点(A在B的左侧),与),轴交于点C.抛物线的对称轴是直线x=﹣2,D是抛物线的顶点.
+mx+4﹣m的图象与x轴交于A、B两点(A在B的左侧),与),轴交于点C.抛物线的对称轴是直线x=﹣2,D是抛物线的顶点.
(1)求二次函数的表达式;
(2)当﹣![]() <x<1时,请求出y的取值范围;
<x<1时,请求出y的取值范围;
(3)连接AD,线段OC上有一点E,点E关于直线x=﹣2的对称点E'恰好在线段AD上,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com