
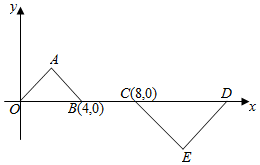
 如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0).
如图所示,等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),则这两个等腰直角三角形的位似中心的坐标为($\frac{16}{3}$,0). 分析 直接利用等腰直角三角形得出MF与FN的关系,进而得出F点坐标.
解答 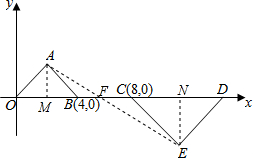 解:过点A作AM⊥x轴于点M,过点E作EN⊥x轴于点N,
解:过点A作AM⊥x轴于点M,过点E作EN⊥x轴于点N,
∵等腰直角三角形OAB和等腰直角三角形CDE是位似图形,点A的坐标为(2,2),点E的坐标为(12,-4),
∴AM=BM=2,CN=NE=4,MN=10,
∴$\frac{MF}{FN}$=$\frac{1}{2}$,
∴MF=$\frac{1}{3}$MN=$\frac{10}{3}$,
∴OM+MF=2+$\frac{10}{3}$=$\frac{16}{3}$,
则这两个等腰直角三角形的位似中心的坐标为:F($\frac{16}{3}$,0),
故答案为:($\frac{16}{3}$,0).
点评 此题主要考查了位似变换以及等腰直角三角形的性质,正确得出MN的长是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 相似三角形面积的比等于相似比的平方,相似多边形面积之比等于相似比的平方.
相似三角形面积的比等于相似比的平方,相似多边形面积之比等于相似比的平方.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
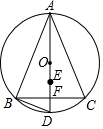 如图,在△ABC中,AB=AC,AD⊥BC于点F,交△ABC外接圆于点D,BC=6,tan∠BAC=$\frac{3}{4}$,点E是△ABC内切圆的圆心,则OE的长为5-$\sqrt{10}$.
如图,在△ABC中,AB=AC,AD⊥BC于点F,交△ABC外接圆于点D,BC=6,tan∠BAC=$\frac{3}{4}$,点E是△ABC内切圆的圆心,则OE的长为5-$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com