
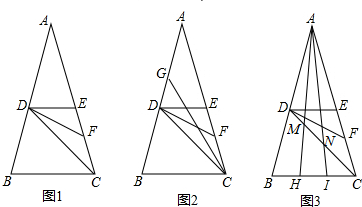
分析 (1)根据DE∥BC,得到∠EDB+∠DBC=180°,再利用角平分线的性质,即可解答;
(2)根据FD⊥AB,∠BGC=50°,得到∠DHG=40°,利用外角的性质得到∠FDC+∠HCD=50°,再根据DF平分∠EDC,CG平分∠ACD,得到∠EDC=2∠FDC,∠ACD=2∠HCD,得到∠EDC+∠ACD=2(∠FDC+∠HCD)=100°,利用三角形内角和为180°,∠DEC=180°-(∠EDC+∠ACD)=180°-100°=80°.
(3)不变,根据∠DMH+∠DEC=2(∠ADF+∠DAN),∠ANF=∠ADF+∠DAN,即可解答.
解答 解:(1)如图1,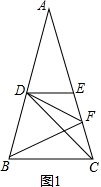
∵DE∥BC,
∴∠EDB+∠DBC=180°,
∴∠EDF+∠FDC+∠CDB+∠DBC=180°,
∵∠CDB=∠DBC,∠EDF=∠FDC,
∴2∠FDC+2∠CDB=180°,
∴∠FDC+∠CDB=90°,
∴FD⊥BD,
∴∠DBF+DFB=90°.
(2)如图2,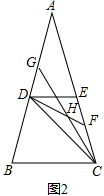
∵∠BGC=50°,FD⊥BD,
∴∠DHG=40°,
∴∠FDC+∠HCD=40°,
∵DF平分∠EDC,CG平分∠ACD,
∴∠EDC=2∠FDC,∠ACD=2∠HCD,
∴∠EDC+∠ACD=2(∠FDC+∠HCD)=80°,
∴∠DEC=180°-(∠EDC+∠ACD)=180°-80°=100°.
(3)不变,如图3,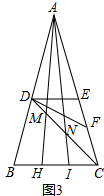
∵∠DMH+∠DEC=2(∠ADF+∠DAN),∠ANF=∠ADF+∠DAN,
∴$\frac{∠DEC+∠DMH}{∠ANF}$=$\frac{2(∠ADF+∠DAN)}{∠ADF+∠DAN}$=2.
点评 本题考查了平行线的性质、三角形角平分线、外角的性质、三角形内角和定理,解决本题的关键是利用三角形的角平分线、外角得到角之间的关系.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
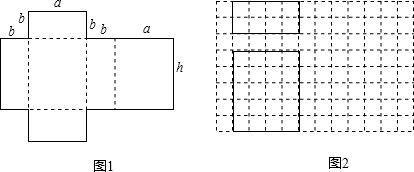
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
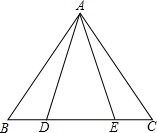 如图,在△ABC中,AB=AC,D、E在BC上,要证明△ABE≌△ACD还应补充的条件是∠AEB=∠ADC或∠BAE=∠CAD或BE=CD或BD=CE(只要求写出一种情况).
如图,在△ABC中,AB=AC,D、E在BC上,要证明△ABE≌△ACD还应补充的条件是∠AEB=∠ADC或∠BAE=∠CAD或BE=CD或BD=CE(只要求写出一种情况).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
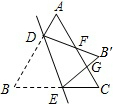 如图,等边三角形ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=95°,则∠EGC的度数为95°.
如图,等边三角形ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=95°,则∠EGC的度数为95°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com