【题目】列方程解应用题
根据城市规划设计，某市工程队准备为该城市修建一条长4800米的公路．铺设600米后，为了尽量减少施工对城市交通造成的影响，该工程队增加人力，实际每天修建公路的长度是原计划的2倍，结果9天完成任务，该工程队原计划每天铺设公路多少米？
【答案】解：设原计划每天铺设公路x米，根据题意，得……………………1分
． ……………………3分
去分母，得 1200+4200=18x（或18x=5400）
解得
． ……………………4分
经检验， 
是原方程的解且符合题意． ……………………5分
答：原计划每天铺设公路300米．
【解析】试题分析：设原计划每天铺设公路x米，根据实际每天修建公路的长度是原计划的2倍，结果9天完成任务，以时间做为等量关系可列方程求解．
试题解析：设原计划每天铺设公路x米，根据题意，得（1分）
去分母，得1200+4200=18x（或18x=5400）
解得x=300．（4分）
经检验，x=300是原方程的解且符合题意．（5分）
答：原计划每天铺设公路300米．
阶梯计算系列答案科目：初中数学 来源： 题型：
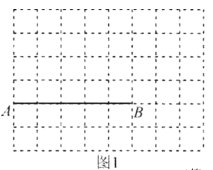
【题目】图1、图2分别是
的网格，网格中每个小正方形的边长均为1，线段
的端点在小正方形的顶点上，请在图1、图2中各画一个图形，分别满足以下要求：
（1）在图1中画一个以线段为一边且周长为
的平行四边形，所画图形的各顶点必须在小正方形的顶点上．
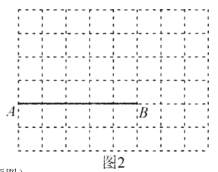
（2）在图2中画一个以线段为一边的等腰钝角三角形，所画等腰三角形的各顶点必须在小正方形的顶点上，并直接写出该等腰三角形的周长是______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（阅读理解）
在解方程组或求代数式的值时，可以用整体代入或整体求值的方法，化难为易．
（1）解方程组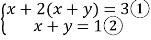
（2）已知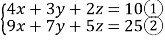
，求x+y+z的值
解：（1）把②代入①得：x+2×1＝3．解得：x＝1．
把x＝1代入②得：y＝0．
所以方程组的解为
，
（2）①×2得：8x+6y+4z＝20．③
②﹣③得：x+y+z＝5．
（类比迁移）
（1）若
，则x+2y+3z＝ ．
（2）解方程组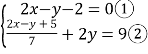
（实际应用）
打折前，买39件A商品，21件B商品用了1080元．打折后，买52件A商品，28件B商品用了1152元，比不打折少花了多少钱？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，（1）正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF＝90°, 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中，BE、DF具有怎样的数量关系和位置关系？结合图(1)给予证明；
(2)将（1）中的正方形ABCD变为矩形ABCD，等腰Rt△AEF变为Rt△AEF，且AD＝kAB,AF＝kAE,其他条件不变.(1)中的结论是否发生变化？结合图(2)说明理由；
(3)将（2）中的矩形ABCD变为平行四边形ABCD，将Rt△AEF变为△AEF，且∠BAD＝∠EAF＝
，其他条件不变.(2)中的结论是否发生变化？结合图(3)，如果不变，直接写出结论；如果变化，直接用k表示出线段BE、DF的数量关系，用
表示出直线BE、DF形成的锐角
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形ABCD中，E为对角线BD的延长线上一点．
（1）求证：AE=CE．
（2）若BC=6，AE=10，∠BAE=120，求BE的长，并直接写出DE的长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y
xb与x轴交于点A，与y轴交于点B，与直线y=x交于点E，点E的横坐标为3．
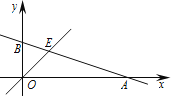
（1）求点A的坐标．
（2）在x轴上有一点P（m，0），过点P作x轴的垂线，与直线yxb交于点C，与直线y=x交于点D．若CD≥5，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在给定的一张平行四边形纸片上按如下操作：连结AC，作AC的垂直平分线MN分别交AD、AC、BC于M、O、N，连结AN，CM，则四边形ANCM是（ ）
A. 矩形 B. 菱形 C. 正方形 D. 无法判断
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：
关于
的方程：
的解为： 
， 
（可变形为
）的解为： 
， 
的解为： 
， 
的解为： 
， 
…………
根据以上材料解答下列问题：
（1）①方程
的解为 ．
②方程
的解为 ．
（2）解关于
方程：
①
（
）
②
（
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线
交 y轴于点为A，顶点为D，对称轴与x轴交于点H．
（1）求顶点D的坐标（用含m的代数式表示）；
（2）当抛物线过点（1，-2），且不经过第一象限时，平移此抛物线到抛物线
的位置，求平移的方向和距离；
（3）当抛物线顶点D在第二象限时，如果∠ADH=∠AHO，求m的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com