
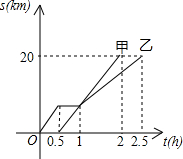
 甲乙两同学在假日期间,义务担任“城市文明宣传员”.两人都从A地出发,骑自行车沿同一条路线宣传,均行驶到B地.他们离出发地距离S(km)与行驶时间t(h)之间的函数关系的图象如图所示.
甲乙两同学在假日期间,义务担任“城市文明宣传员”.两人都从A地出发,骑自行车沿同一条路线宣传,均行驶到B地.他们离出发地距离S(km)与行驶时间t(h)之间的函数关系的图象如图所示.分析 (1)利用总路程除以总时间得出乙的平均速度;
(2)首先求出甲行驶路程距A地的函数关系式,进而利用当x=1时,y=$\frac{20}{3}$,得出答案即可;
(3)求得2h后乙和甲的距离,以及他们两人的速度,再根据路程和÷速度和=时间,列式计算即可求解;
(4)分四种情况:第一种:乙出发而甲未出发;第二种:乙停留时甲出发;第三种:两人相遇之后且甲未到达B地,;第四种:甲到达B地而乙未到达;讨论即可求解.
解答 解:(1)20÷2.5=8(千米/小时),
故答案为:8千米/小时;
(2)设甲行驶路程距A地的函数关系式为:y=kx+b,
把(0.5,0),(2,20)代入y=kx+b得:
$\left\{\begin{array}{l}{0.5k+b=0}\\{2k+b=20}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{40}{3}}\\{b=-\frac{20}{3}}\end{array}\right.$,
∴y=$\frac{40}{3}x-\frac{20}{3}$,
当x=1时,y=$\frac{40}{3}-\frac{20}{3}=\frac{20}{3}$,
∴甲、乙相遇时,他们离出发地的距离为$\frac{20}{3}$千米;
(3)(20-$\frac{20}{3}$)÷(1.5÷1)
=$\frac{40}{3}$÷1.5
=$\frac{80}{9}$km,
20-$\frac{20}{3}$-$\frac{80}{9}$=$\frac{40}{9}$km,
$\frac{40}{9}$÷[$\frac{20}{3}$÷0.5+(20-$\frac{20}{3}$)÷1.5]
=$\frac{40}{9}$÷[$\frac{40}{3}$+$\frac{80}{9}$]
=$\frac{40}{9}$÷$\frac{200}{9}$
=0.2小时.
故还需要0.2小时时间才能再次与小李相遇.
(4)第一种:乙出发而甲未出发,$\frac{3}{40}$小时后,两人相距1km;
第二种:乙停留时甲出发,$\frac{37}{40}$小时后,两人相距1km;
第三种:两人相遇之后且甲未到达B地,$\frac{49}{40}$小时后,两人相距1km;
第四种:甲到达B地而乙未到达,$\frac{191}{80}$小时后,两人相距1km.
点评 本题考查了一次函数的运用,解决本题的关键是学会看函数图象,理解函数图象所反映的实际意义,从函数图象中获取信息,并且解决有关问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
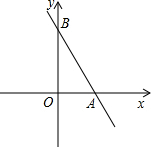 直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,M是y轴上一点,若将△ABM沿AM折叠,点B恰好落在x轴上,则点M的坐标为(0,$\frac{3}{2}$)或(0,-6).
直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,M是y轴上一点,若将△ABM沿AM折叠,点B恰好落在x轴上,则点M的坐标为(0,$\frac{3}{2}$)或(0,-6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 14:00 | B. | 14:20 | C. | 14:30 | D. | 14:40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
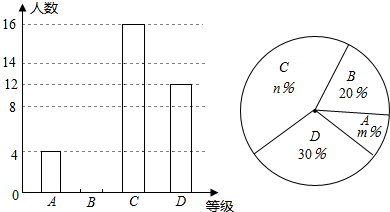
| A. | 参加演讲比赛学生共40人 | |
| B. | 扇形统计图中m=10,n=40 | |
| C. | 学校欲从获A等级的学生中随机选取2人参加市级比赛,选中A等级的小明的概率为$\frac{1}{2}$ | |
| D. | C等级所对应的圆心角为120度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com