
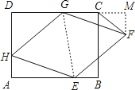
【题目】如图,已知在矩形ABCD中,AD=6,DC=7,点H为AD上一点,并且AH=2,点E为AB上一动点,以HE为边长作菱形HEFG,并且使点G在CD边上,连接CF
(1)如图1,当DG=2时,求证:四边形EFGH为正方形;
(2)如图2,当DG=6时,求△CGF的面积;
(3)当DG的长度为何值时,△CGF的面积最小,并求出△CGF面积的最小值;

【答案】(1)证明见解析(2)1(3)当DG=![]() 时,△FCG的面积最小为(7-
时,△FCG的面积最小为(7-![]() )
)
【解析】
(1)由于四边形ABCD为矩形,四边形HEFG为菱形,可得∠D=∠A=90°,HG=HE;已知AH=DG=2,易证△AHE≌△DGH,由全等三角形的性质可得∠DHG=∠HEA,再证得∠EHG=90°,即可判定四边形HEFG为正方形;(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于AB∥CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,从而有FM=HA=2(即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2),进而可求三角形面积;(3)先设DG=x,由第(2)小题得,S△FCG=7-x,在△AHE中,AE≤AB=7,利用勾股定理可得HE2≤53,在Rt△DHG中,再利用勾股定理可得x2+16≤53,进而可求x≤![]() ,从而可得当x=
,从而可得当x=![]() 时,△GCF的面积最小,由此即可解答.
时,△GCF的面积最小,由此即可解答.
(1)∵四边形ABCD为矩形,四边形HEFG为菱形,
∴∠D=∠A=90°,HG=HE,又AH=DG=2,
∴Rt△AHE≌Rt△DGH(HL),
∴∠DHG=∠HEA,
∵∠AHE+∠HEA=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形HEFG为正方形;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,
∵AB∥CD,
∴∠AEG=∠MGE,
∵HE∥GF,
∴∠HEG=∠FGE,
∴∠AEH=∠MGF,
在△AHE和△MFG中,∠A=∠M=90°,HE=FG,
∴△AHE≌△MFG,
∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,
因此S△FCG=![]() ×FM×GC=
×FM×GC=![]() ×2×(7-6)=1;
×2×(7-6)=1;
(3)设DG=x,则由第(2)小题得,S△FCG=7-x,在△AHE中,AE≤AB=7,
∴HE2≤53,
∴x2+16≤53,
∴x≤![]() ,
,
∴S△FCG的最小值为7-![]() ,此时DG=
,此时DG=![]() ,
,
∴当DG=![]() 时,△FCG的面积最小为(7-
时,△FCG的面积最小为(7-![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
(1)数轴上表示2和10两点之间的距离是_______.
(2)数轴上一个点到表示2的点的距离为5.2,这个点表示的数为______.
(3)若x表示一个数,数轴上表示x和﹣5的两点之间的距离是____;(用含x的式子表示)
(4)若x表示一个数,|x+1|+|x﹣2|的最小值是______,相应的x的取值范围_______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
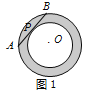
【题目】(1)如图1,同心圆中,大圆O的弦AB与小圆O切于点P,且AB=16,则圆环面积为________;
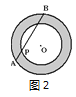
(2)如图2,同心圆中,大圆O的弦AB与小圆O相交,其中一个交点为点P,且AP=2,PB=8,则圆环面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,
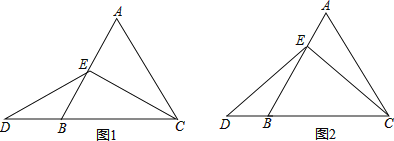
(1)当点E为AB的中点时,如图1,求证:EC=ED;
(2)当点E不是AB的中点时,如图2,过点E作EF//BC,求证:△AEF是等边三角形;
(3)在第(2)小题的条件下,EC与ED还相等吗,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
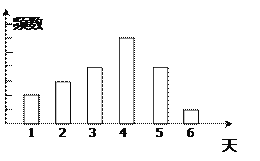
【题目】某公司对用户满意度进行问卷调查,将连续6天内每天收回的问卷数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第3天的频数是12.请你回答:
(1)收回问卷最多的一天共收到问卷_________份;
(2)本次活动共收回问卷共_________份;
(3)市场部对收回的问卷统一进行了编号,通过电脑程序随机抽选一个编号,抽到问卷是第4天收回的概率是多少?
(4)按照(3)中的模式随机抽选若干编号,确定幸运用户发放纪念奖,第4天和第6天分别有10份和2份获奖,那么你认为这两组中哪个组获奖率较高?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划开设4门选修课:音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),对调查结果进行统计后,绘制了如下不完整的两个统计图.
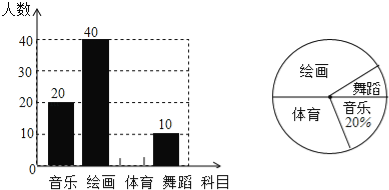
根据以上统计图提供的信息,回答下列问题:
(1)此次调查抽取的学生人数为a= 人,其中选择“绘画”的学生人数占抽样人数的百分比为b= ;
(2)补全条形统计图;
(3)若该校有2000名学生,请估计全校选择“绘画”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂有甲、乙、丙三个蓄水池,已知甲蓄水池的蓄水量x是从3万吨至6万吨,乙蓄水池的蓄水量y万吨与甲蓄水池蓄水量x万吨之间的关系是: ![]() ,丙蓄水池的蓄水量的3倍恰好是甲蓄水池的蓄水量与乙蓄水池的蓄水量的积.问:
,丙蓄水池的蓄水量的3倍恰好是甲蓄水池的蓄水量与乙蓄水池的蓄水量的积.问:
(1)若丙蓄水池的蓄水量最大为22万吨,当甲蓄水池的蓄水量为6吨时, 丙蓄水池能否容纳?为什么?
(2)求丙蓄水池的蓄水量z万吨与甲蓄水池蓄水量x万吨之间的关系?
(3)蓄水池管理员在观察三个蓄水池蓄水量的记录时发现,在整个蓄水过程中, 丙蓄水池的蓄水量多次出现整数万吨的情况,你能说出共出现过多少次?分别是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数前的序号分别填入相应的集合内:
①-2.5, ②0,③![]() ,④
,④![]() ,⑤
,⑤![]() ,⑥
,⑥![]() ,⑦-0.5252252225…(每两个5之间依次增加1个2).
,⑦-0.5252252225…(每两个5之间依次增加1个2).
(1)正数集合: { …};
(2)负分数集合:{ …};
(3)整数集合: { …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com