
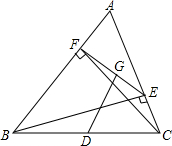
 BE、CF为△ABC的二高,D为BC中点,BG⊥EF,求证:
BE、CF为△ABC的二高,D为BC中点,BG⊥EF,求证:科目:初中数学 来源: 题型:
 如图,在B港有“远望1号”和“远望2号”两艘轮船同时出发,若“远望1号”轮船沿北偏东60°方向每小时行驶8n mile,“远望2号”轮船沿南偏东30°方向每小时行驶15n mile,两小时后,两艘轮船分别到达M岛和N岛,求M岛和N岛之间的距离.
如图,在B港有“远望1号”和“远望2号”两艘轮船同时出发,若“远望1号”轮船沿北偏东60°方向每小时行驶8n mile,“远望2号”轮船沿南偏东30°方向每小时行驶15n mile,两小时后,两艘轮船分别到达M岛和N岛,求M岛和N岛之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,三个村庄A,B,C之间的距离分别为BC=5km,AC=12km,AB=13km.现准备从C村修一条公路CD直达公路AB,已知公路的造价为39000元/km,求修这条公路的最低造价是多少?
如图,三个村庄A,B,C之间的距离分别为BC=5km,AC=12km,AB=13km.现准备从C村修一条公路CD直达公路AB,已知公路的造价为39000元/km,求修这条公路的最低造价是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
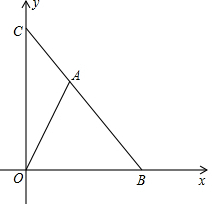 如图,已知点B的坐标为(4,0)点C的坐标为(0,4)点A在线段BC上,且不与点B,C重合.
如图,已知点B的坐标为(4,0)点C的坐标为(0,4)点A在线段BC上,且不与点B,C重合.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com