练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列方程没有实数根的是（　　）

    A. x3+2＝0B. x2+2x+2＝0

    C. ＝x﹣1D. ＝0

    【答案】B

    【解析】

    根据立方根的定义即可判断A；根据根的判别式即可判断B；求出方程x2-3=（x-1）2的解，即可判断C；求出x-2=0的解，即可判断D．

    A、x3+2＝0，

    x3＝﹣2，

    x＝﹣，即此方程有实数根，故本选项不符合题意；

    B、x2+2x+2＝0，

    △＝22﹣4×1×2＝﹣4＜0，

    所以此方程无实数根，故本选项符合题意；

    C、＝x﹣1，

    两边平方得：x2﹣3＝（x﹣1）2，

    解得：x＝2，

    经检验x＝2是原方程的解，即原方程有实数根，故本选项不符合题意；

    D、＝0，

    去分母得：x﹣2＝0，

    解得：x＝2，

    经检验x＝2是原方程的解，即原方程有实数根，故本选项不符合题意；

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】钓鱼岛是我国的神圣领土，中国人民维护国家领土完整的决心是坚定的，多年来，我国的海监、渔政等执法船定期开赴钓鱼岛巡视．某日，我海监船（A处）测得钓鱼岛（B处）距离为20海里，海监船继续向东航行，在C处测得钓鱼岛在北偏东45°的方向上，距离为10海里，求AC的距离．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列各式：

    13＝×12×22

    13+23＝9＝×22×32

    13+23+33＝36＝×32×42

    13+23+33+43＝100＝×42×52

    回答下面的问题：

    (1)猜想：13+23+33+…+(n－1)3+ n3＝________.

    (2)利用你得到的(1)中的结论，计算13+23+33+…+993+1003的值.

    (3)计算：213+223+…+993+1003的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，抛物线y=mx2﹣2mx+n（m＜0）的顶点为A，与x轴交于B，C两点（点B在点C左侧），与y轴正半轴交于点D，连接AD并延长交x轴于E，连AC、DC．S△DEC：S△AEC=3：4．

    （1）求点E的坐标；

    （2）△AEC能否为直角三角形？若能，求出此时抛物线的函数表达式；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点P（1，m）、Q（n，1）在反比例函数y＝的图象上，直线y＝kx+b经过点P、Q，且与x轴、y轴的交点分别为A、B两点．

    （1）求 k、b的值；

    （2）O为坐标原点，C在直线y＝kx+b上且AB＝AC，点D在坐标平面上，顺次联结点O、B、C、D的四边形OBCD满足：BC∥OD，BO＝CD，求满足条件的D点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为了美化环境，计划在一定的时间内完成绿化面积万亩的任务，后来市政府调整了原定计划，不但绿化面积要在原计划的基础上增加，而且要提前年完成任务，经测算要完成新的计划，平均每年的绿化面积必须比原计划多万亩，求原计划平均每年的绿化面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，ABCD为正方形，将正方形的边CB绕点C顺时针旋转到CE，记∠BCE=α，连接BE，DE，过点C作CF⊥DE于F，交直线BE于H．

    （1）当α=60°时，如图1，则∠BHC= ；

    （2）当45°＜α＜90°，如图2，线段BH、EH、CH之间存在一种特定的数量关系，请你通过探究，写出这个关系式： （不需证明）；

    （3）当90°＜α＜180°，其它条件不变（如图3），（2）中的关系式是否还成立？若成立，说明理由；若不成立，写出你认为成立的结论，并简要证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在学习了正方形之后，给同桌小文出了道题．从下列四个条件：①AB＝BC；②∠ABC＝90°；③AC＝BD；④AC⊥BD中选出两个作为补充条件，使平行四边形ABCD成为正方形(如图所示)．现有下列四种选法，你认为其中错误的是( )

    A. ①②B. ②④C. ①③D. ②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

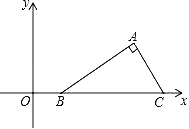
    【题目】如图，在平面直角坐标系中Rt△ABC的斜边BC在x轴上，点B坐标为（1，0），AC=2，∠ABC=30°，把Rt△ABC先绕B点顺时针旋转180°，然后再向下平移2个单位，则A点的对应点A′的坐标为（　　）

    A. （﹣4，﹣2﹣） B. （﹣4，﹣2+） C. （﹣2，﹣2+） D. （﹣2，﹣2﹣）

    查看答案和解析>>

    同步练习册答案