
如图,一次函数y=kx+n的图象与x轴和y轴分别交于点A(6,0)和B(0, ),线段AB的垂直平分线交x轴于点C,交AB于点D.
),线段AB的垂直平分线交x轴于点C,交AB于点D.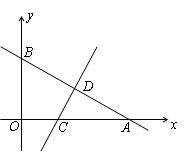
(1)试确定这个一次函数解析式;(3分)
(2)求过A、B、C三点的抛物线的函数关系式;(6分)
(3)请你利用所求抛物线的图像回答:当x取何值时,抛物线中的部分图像落在x轴的上方? (3分)
(1) ;(2)
;(2) ;(3)
;(3) 或
或 .
.
解析试题分析:(1)根据A、B的坐标用待定系数法即可求出直线AB的解析式;(2)根据A、B的坐标求出AB的长,即可求出AD的值,然后在Rt△ACD中根据∠DAC的余弦值求出AC的长,即可求出OC的长也就能求出C点的坐标,然后用待定系数法求出抛物线的解析式;(3)由于抛物线开口向上,与x轴的交点为A,C,所以当 或
或 时,抛物线中的部分图像落在x轴的上方.
时,抛物线中的部分图像落在x轴的上方.
试题解析:(1)∵一次函数 的图象与x轴和y轴分别交于点A(6,0)和B(0,
的图象与x轴和y轴分别交于点A(6,0)和B(0, ),
),
∴ ,解得
,解得 .
.
∴这个一次函数关系式为 .
.
(2)根据A、B的坐标可得OA=6,OB= ,∴AB=
,∴AB= ,∠BAO=30°.
,∠BAO=30°.
∵CD是线段AB的垂直平分线,∴AD= .
.
在Rt△ACD中,AD= ,∠BAO=30°,∴
,∠BAO=30°,∴ ,OC=OA-AC="2." ∴C(2,0).
,OC=OA-AC="2." ∴C(2,0).
设抛物线的解析式为 ,将B点坐标代入后得:
,将B点坐标代入后得: .
.
∴抛物线的解析式为: ,即
,即 .
.
(3)当 或
或 时,抛物线中的部分图像落在x轴的上方.
时,抛物线中的部分图像落在x轴的上方.
考点:1.二次函数综合题;2.待定系数法;3.曲线上点的坐标与方程的关系;4.勾股定理;5.线段垂直平分线的性质;6.锐角三角函数定义;7.特殊角的三角函数值.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
二次函数的图象经过点 ,
, ,
, .
.
(1)求此二次函数的关系式;
(2)求此二次函数图象的顶点坐标;
(3)填空:把二次函数的图象沿坐标轴方向最少平移 个单位,使得该图象的顶点在原点.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线y=x2-2kx+3k+4.
(1)顶点在y轴上时,k的值为_________.
(2)顶点在x轴上时,k的值为_________.
(3)抛物线经过原点时,k的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数图象的顶点是(-1,2),且过点(0, ).
).
(1)求二次函数的表达式,并在图中画出它的图象;
(2)判断点(2, )是否在该二次函数图象上;并指出当
)是否在该二次函数图象上;并指出当 取何值时,
取何值时,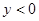 ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线 上有一点M(x0,
上有一点M(x0, )位于
)位于 轴下方.
轴下方.
(1)求证:此抛物线与x轴交于两点;
(2)设此抛物线与 轴的交点为A(
轴的交点为A( ,0),B(
,0),B( ,0),且
,0),且 <
< ,求证:
,求证: <
< <
< .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与直线
与直线 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.
(1)求点A、B的坐标;
(2)若点P是直线x=1上一点,是否存在△PAB是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
(1)求该抛物线的解析式;
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com