
【题目】如图,E、F是平行四边形ABCD对角线AC上两点,AE=CF.
证明(1)△ABE≌△CDF;
(2)BE∥DF.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
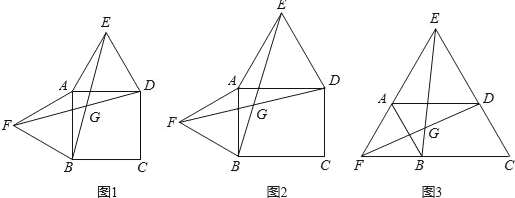
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)单项式﹣2x3ym与5xn+1y的差是一个单项式,求![]() 的值;
的值;
(2)化简求值:(x2+5﹣4x3)﹣2(﹣2x3+5x﹣4),其中x=﹣2;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,
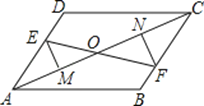
求证:(1)EM=FN;
(2)EF与MN互相平分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.
![]()
(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程的特征及其解的特点.
①x+![]() =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+![]() =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+![]() =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为________,其解为________;
(2)根据这类方程的特征,写出第n个方程为________,其解为________;
(3)请利用(2)的结论,求关于x的方程x+![]() =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com