
| A. | (2,1) | B. | (2,-1) | C. | (1,-2) | D. | (0,5) |
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
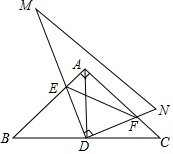 将一副三角板按如图摆放,其中△ABC为含有45度角的三角板,直线AD是等腰直角三角形ABC的对称轴,且将△ABC分成两个等腰直角三角形,DM、DN分别与边AB、AC交于E、F两点,有下列四个结论:①BD=AD=CD②△AED≌△CFD③BE+CF=EF④S四边形AEDF=$\frac{1}{4}$AB2.其中正确结论是①②④(填写正确序号)
将一副三角板按如图摆放,其中△ABC为含有45度角的三角板,直线AD是等腰直角三角形ABC的对称轴,且将△ABC分成两个等腰直角三角形,DM、DN分别与边AB、AC交于E、F两点,有下列四个结论:①BD=AD=CD②△AED≌△CFD③BE+CF=EF④S四边形AEDF=$\frac{1}{4}$AB2.其中正确结论是①②④(填写正确序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
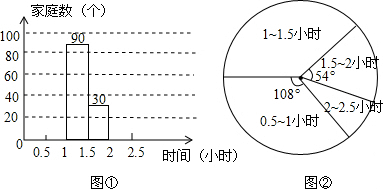
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
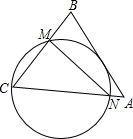 如图,在△ABC中,∠BCA=60°,∠A=45°,AC=2$\sqrt{6}$,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是3.
如图,在△ABC中,∠BCA=60°,∠A=45°,AC=2$\sqrt{6}$,经过点C且与边AB相切的动圆与CB,CA分别相交于点M,N,则线段MN长度的最小值是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
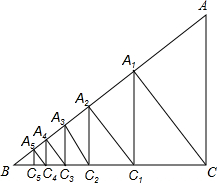 如图,已知直角△ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段A1C1,A2C2…,则线段AnCn为3×($\frac{4}{5}$)2n.(用含有n的代数式表示)
如图,已知直角△ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段A1C1,A2C2…,则线段AnCn为3×($\frac{4}{5}$)2n.(用含有n的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
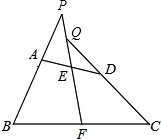 如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
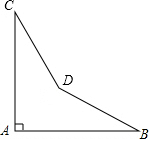 某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?
某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com