
【题目】列方程解应用题:某校组织七年级师生共300人乘车前往“故乡”农场进行劳动教育活动.
(1)他们早晨8:00从学校出发,原计划当天上午10:00便可以到达“故乡”农场,但实际上他们当天上午9:40便达到了“故乡”农场,已知汽车实际行驶速度比原计划行驶速度快10km/h.求汽车原计划行驶的速度.
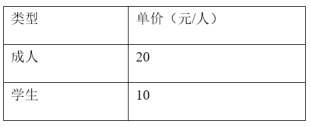
(2)到达“故乡”农场后,需要购买门票,已知该农场门票票价情况如右表,该校购买门票时共花了3100元,那么参加此次劳动教育的教师、学生各多少人?
科目:初中数学 来源: 题型:
【题目】已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
![]()
请写出AB中点M对应的数。
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动。设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动。设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平整的地面上,用若干个完全相同的棱长为10 cm的小正方体堆成一个几何体.
(1)现已给出这个几何体的俯视图(如图②),请你画出这个几何体的主视图与左视图;
(2)若现在你手头还有一些相同的小正方体,如果保持这个几何体的主视图和俯视图不变.
①在图①所示的几何体中最多可以再添加几个小正方体?
②在图①所示的几何体中最多可以拿走几个小正方体?
③在②的情况下,把这个几何体放置在墙角,如图③所示是此时这个几何体放置的俯视图,若给这个几何体表面喷上红漆,则需要喷漆的面积最少是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:![]() ;
;![]() 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若![]() >0,
>0,![]() >0,则
>0,则![]() >0;若
>0;若![]() <0,
<0,![]() <0,则
<0,则![]() >0;
>0;
(2)若![]() >0,
>0,![]() <0,则
<0,则![]() <0;若
<0;若![]() <0,
<0,![]() >0,则
>0,则![]() <0.
<0.
反之:(1)若![]() >0,则
>0,则![]() 或
或![]()
(2)若![]() <0,则__________或__________.
<0,则__________或__________.
(3)根据上述规律,求不等式![]() 的解集.
的解集.
(4)试求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
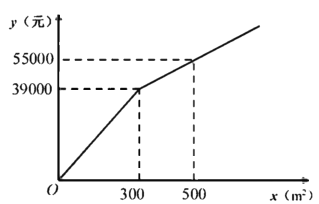
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
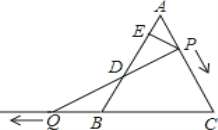
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
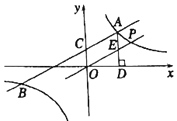
【题目】如图,一次函数y1=k1x+2与反比例函数y2=![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= ,k2= ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求直线OP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连结CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
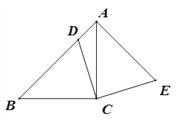
(1)求证:AB⊥AE;
(2)若![]() ,求证:四边形ADCE为正方形.
,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com