
 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,若点P的坐标为(-2,t),当PA=AB时,求点A的坐标.
如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,若点P的坐标为(-2,t),当PA=AB时,求点A的坐标. 分析 首先求出P点坐标,再利用梯形的性质得出B点坐标,代入y=x2求出m的值即可得出A点坐标.
解答 解:∵点P(-2,t)在直线y=-2x-2上,
∴t=2,
∴P(-2,2).
设A(m,m2),
如图所示,分别过点P、A、B 作x轴垂线,垂足分别为点G、E、F.
作x轴垂线,垂足分别为点G、E、F.
∵PA=AB,∴AE是梯形PGFB的中位线,
∴GE=EF,AE=$\frac{1}{2}$(PG+BF).
∵OF=|EF-OE|,GE=EF,
∴OF=|GE-EO|,
∵GE=GO-EO=2+m,EO=-m,
∴OF=|2+m-(-m)|=|2+2m|,
∴OF=2m+2,
∵AE=$\frac{1}{2}$(PG+BF),
∴BF=2AE-PG=2m2-2,
∴B(2+2m,2m2-2).
∵点B在抛物线y=x2上,
∴2m2-2=(2+2m)2
解得:m=1或-3,
当m=-1时,m2=1;当m=-3时,m2=9
故点A的坐标为(-1,1)或(-3,9).
点评 本题主要考查了二次函数的性质,解答本题的关键是正确地作出辅助线,求出点B的坐标,此题有一定的难度.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 220 | B. | 200 | C. | 120 | D. | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
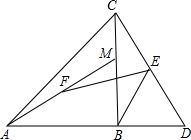 如图,在等腰直角△ABC中,AB=BC,点M是BC边上任意一点,点D是AB的延长线上一点,且BM=BD;又有点E、F分别是CD、AM边的中点,连结FE、EB.下列结论一定正确的有( )
如图,在等腰直角△ABC中,AB=BC,点M是BC边上任意一点,点D是AB的延长线上一点,且BM=BD;又有点E、F分别是CD、AM边的中点,连结FE、EB.下列结论一定正确的有( )| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com