
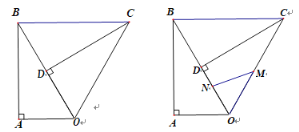
【题目】已知Rt△OAB,OAB90,ABO30,斜边OB4,将Rt△OAB绕点O顺时针旋转60,得到△COD,如图1,连接BC.
(1)求BC的长度;
(2)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿OCB路径匀速运动,N沿OBC路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5个单位/秒,点N的运动速度为1个单位/秒,设运动时间为x秒,△OMN的面积为y,求y关于x的函数解析式,并直接写出自变量x的取值范围.
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() 为
为![]() 边上一点.
边上一点.
(1)当![]() 时,直接写出
时,直接写出![]() ,
,![]() .
.
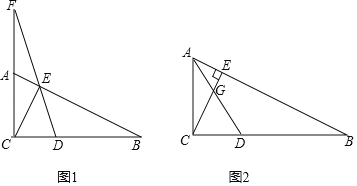
(2)如图1,当![]() ,
,![]() 时,连
时,连![]() 并延长交
并延长交![]() 延长线于
延长线于![]() ,求证:
,求证:![]() .
.
(3)如图2,连![]() 交
交![]() 于
于![]() ,当
,当![]() 且
且![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
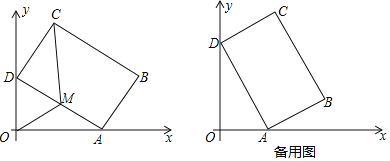
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为![]() 时,求OA的长;
时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A(2,1),B两点.
的图象相交于A(2,1),B两点.

(1)求出反比例函数与一次函数的表达式;
(2)请直接写出B点的坐标,并指出使反比例函数值大于一次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
(1)等边三角形“內似线”的条数为 ;
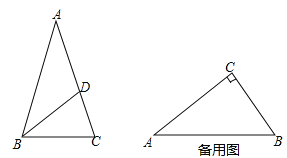
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图1,正方形ABCD的对角线交于点O,△CDE是边长为6的等边三角形,则O、E之间的距离为 ;
问题探究
(2)如图2,在边长为6的正方形ABCD中,以CD为直径作半圆O,点P为弧CD上一动点,求A、P之间的最大距离;
问题解决
(3)窑洞是我省陕北农村的主要建筑,窑洞宾馆更是一道靓丽的风景线,是因为窑洞除了它的坚固性及特有的外在美之外,还具有冬暖夏凉的天然优点家住延安农村的一对即将参加中考的双胞胎小宝和小贝两兄弟,发现自家的窑洞(如图3所示)的门窗是由矩形ABCD及弓形AMD组成,AB=2m,BC=3.2m,弓高MN=1.2m(N为AD的中点,MN⊥AD),小宝说,门角B到门窗弓形弧AD的最大距离是B、M之间的距离.小贝说这不是最大的距离,你认为谁的说法正确?请通过计算求出门角B到门窗弓形弧AD的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了正多边形之后,小马同学发现利用对称、旋转等方法可以计算等分正多边形面积的方案.
(1)请聪明的你将下面图①、图②、图③的等边三角形分别割成2个、3个、4个全等三角形;
(2)如图④,等边△ABC边长AB=4,点O为它的外心,点M、N分别为边AB、BC上的动点(不与端点重合),且∠MON=120°,若四边形BMON的面积为s,它的周长记为l,求![]() 最小值;
最小值;
(3)如图⑤,等边△ABC的边长AB=4,点P为边CA延长线上一点,点Q为边AB延长线上一点,点D为BC边中点,且∠PDQ=120°,若PA=x,请用含x的代数式表示△BDQ的面积S△BDQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
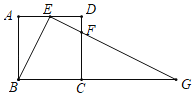
【题目】如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G.
(1)求证:△ABE∽△EGB.
(2)若AB=4,求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com