
分析 因为$\sqrt{8}$=2,所以首先作出以1为直角边的等腰直角三角形,则其斜边即是$\sqrt{2}$.以原点为圆心,以2$\sqrt{2}$为半径画弧,和数轴的正半轴交于一点即可.
作一个直角三角形,两直角边长分别是1和1,这个直角三角形的斜边长就是$\sqrt{2}$,然后在数轴上表示出$\sqrt{3}$即可.
解答 解:如图所示,点A即为所求作的点.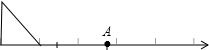
如图所示: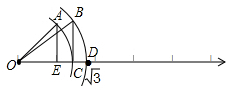
①作出$\sqrt{2}$所表示的点:首先过表示1的点E作垂线,再截取AE=1,然后连接OA,再以O为圆心,OA长为半径画弧,与原点右边的坐标轴的交点C为$\sqrt{2}$.
②作出$\sqrt{3}$所表示的点:过点C作BC⊥OC,在BC上截取BC=1,连接OB,以O为圆心,OB长为半径作弧,与原点右边的数轴交点D为$\sqrt{3}$.
点评 本题考查了勾股定理,无理数用数轴上的点表示的方法,能够熟练运用勾股定理进行计算.


科目:初中数学 来源: 题型:解答题
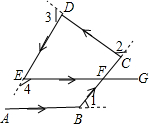 如图,汽车沿“A→B→C→D→E→F”前进过程中,经过四次转弯后与原来方向相同,四次转完的角度分别为∠1、∠2、∠3、∠4,求∠1+∠2+∠3+∠4的度数.
如图,汽车沿“A→B→C→D→E→F”前进过程中,经过四次转弯后与原来方向相同,四次转完的角度分别为∠1、∠2、∠3、∠4,求∠1+∠2+∠3+∠4的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a$\sqrt{x}$-b$\sqrt{y}$ | B. | b$\sqrt{x}$-a$\sqrt{y}$ | C. | $\sqrt{y}$-$\sqrt{x}$ | D. | $\sqrt{y}$+$\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AD=BC,AB=DC | B. | OA=OC,OB=OD | C. | AB∥DC,AD=BC | D. | ∠A=∠C,∠B=∠D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com