
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC对角线的交点为M,分别与AB,BC交于点D,E,连接OD,OE,则$\frac{CE}{EB}$=$\frac{1}{3}$,当k=4时,四边形ODBE的面积为12平方单位.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC对角线的交点为M,分别与AB,BC交于点D,E,连接OD,OE,则$\frac{CE}{EB}$=$\frac{1}{3}$,当k=4时,四边形ODBE的面积为12平方单位. 分析 设B(a,b),则E($\frac{k}{b}$,b),D(a,$\frac{k}{a}$),M($\frac{1}{2}$a,$\frac{1}{2}$b),得出k=$\frac{1}{2}$a•$\frac{1}{2}$b=$\frac{ab}{4}$,得出ab=4k,即可求得$\frac{CE}{EB}$=$\frac{1}{3}$;然后分别找出△OCE、△OAD、矩形OABC的面积与k的关系,列出等式求出即可求得四边形ODBE的面积.
解答 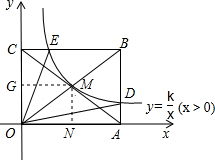 解:设B(a,b),
解:设B(a,b),
∴E($\frac{k}{b}$,b),D(a,$\frac{k}{a}$),M($\frac{1}{2}$a,$\frac{1}{2}$b),
∴k=$\frac{1}{2}$a•$\frac{1}{2}$b=$\frac{ab}{4}$,
∴ab=4k,
∴$\frac{CE}{EB}$=$\frac{\frac{k}{b}}{a-\frac{k}{b}}$=$\frac{\frac{k}{b}}{\frac{ab-k}{b}}$=$\frac{\frac{k}{b}}{\frac{4k-k}{b}}$=$\frac{1}{3}$;
∵E、M、D位于反比例函数图象上,
则S△OCE=$\frac{k}{2}$=2,S△OAD=$\frac{k}{2}$=2,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=k,
又∵M为矩形ABCO对角线的交点,
∴S矩形ABCO=4S□ONMG=4k=16,
∴2+2+S四边形ODBE=16,
解得:S四边形ODBE=12.
故答案为$\frac{1}{3}$;12.
点评 本题考查了反比例函数综合题:先设反比例函数图象上某点的坐标,然后利用矩形的性质和反比例函数图象上点的坐标特点表示其它有关点的坐标,然后利用面积公式建立等量关系,从而解决问题.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
 如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题.
如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
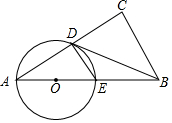 如图,在Rt△ABC中,∠C=90°,点D是AC的中点,过点A、D作⊙O,⊙O与AB交于点E,AE是⊙O的直径,AD是⊙O的一条弦,且∠A+∠CDB=90°,AD:AE=4:5,BC=6.
如图,在Rt△ABC中,∠C=90°,点D是AC的中点,过点A、D作⊙O,⊙O与AB交于点E,AE是⊙O的直径,AD是⊙O的一条弦,且∠A+∠CDB=90°,AD:AE=4:5,BC=6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.56×10-5 | B. | 1.56×10-6 | C. | 1.56×10-7 | D. | 15.6×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元/件) | 30 | 31 | … | 70 |
| y(万件) | 120 | 119 | … | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com