
【题目】如图,已知在正方形ABCD中,F是CD边上一点(不与C、D重合),过点D作DG⊥BF交BF延长线于点G.连接AG,交BD于点E,交CD于点M,连接EF.若DG=4,AG=![]() ,则EF的长为____________.
,则EF的长为____________.

【答案】![]()
【解析】试题分析:
如图作AH⊥BG于H交BC于T,AN⊥GD于N,取BD的中点O,连接OA、OG.
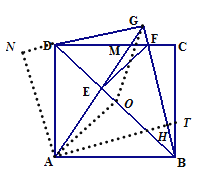
∴∠BAD=∠BGD=90°,
∴OA=OD=OB=OG,
∴A、B、G、D四点共圆,
∴∠AGB=∠ADB=45°,∠AGD=∠ABD=45°,
∴AH=GH,AN=NG,
∵∠N=∠AHG=∠HGN=90°,
∴四边形ANGH是矩形,∵AH=HG,
∴四边形ANGH是正方形,
∵AG=![]() ,
,
∴AH=HG=GN=AN=5,
易证△AND≌△AHB,
∴DN=BH,
∴GD+GB=GN-DN+GH+BH=2GN=10,
∴4+GB=10,
∴GB=6,BD=![]() =
=![]() =
=![]() ,
,
∴BH=1,
∵△BHT∽△AHB,
∴BH2=AHHT,
∴HT=![]() ,
,
∴AT=AH+TH=![]() ,
,
易证△ABT≌△BCF,
∴AT=BF=![]() ,
,
∵△BEF∽△BGD,
∴![]() ,
,
∴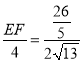 ,
,
∴EF=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
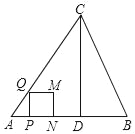
【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)直接写出tanB的值为 .
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为1:3两部分时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以ABCD 的四条边为边,分别向外作正方形,连结 EF,GH,IJ,KL.如果ABCD 的 面积为 8,则图中阴影部分四个三角形的面积和为( )

A.8B.12C.16D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着网络的发展,我们的生活越来越方便,越来越多的人在网络上购物,微商这个行业也悄然兴起,很多人通过微信平台销售商品.
(1)某水果微商今年九月购进榴莲和奇异果共1000千克,它们的进价均为每千克24 元,然后以榴莲售价每千克45元,奇异果售价每千克36元的价格很快销售完,若该水果微商九月获利不低于17400元,求应购进榴莲至少多少千克?
(2)为了增加销售量,获得更大的利润,在进价不变的情况下,该水果微商十月决定调整售价,榴莲的售价在九月的基础上下调![]() (降价后的售价不低于进价),奇异果的售价在九月的基础上上涨
(降价后的售价不低于进价),奇异果的售价在九月的基础上上涨![]() ,同时,与(1)中获得的最低利润时的销售量相比,榴莲的销售量下降了
,同时,与(1)中获得的最低利润时的销售量相比,榴莲的销售量下降了![]() ,而奇异果的销售量上升了
,而奇异果的销售量上升了![]() ,结果十月的销售额比九月增加了600元.求
,结果十月的销售额比九月增加了600元.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④![]() 。其中正确的结论有( )
。其中正确的结论有( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距4800米,甲从A地出发步行到B地,20分钟后乙从B地出发骑自行车到A地,设甲步行的时间为x分钟,甲、乙两人离A地的距离分别为![]() 米、
米、![]() 米,
米,![]() 、
、![]() 与x的函数关系图象如图所示,根据图象解答下列问题:
与x的函数关系图象如图所示,根据图象解答下列问题:

(1)直接写出y![]() 、y
、y![]() 与x的函数关系式,并写出自变量x的取值范围;
与x的函数关系式,并写出自变量x的取值范围;
(2)求甲出发后多少分钟两人相遇,相遇时乙离A地多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com