练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    23、如图所示，有一个正方体，在它的各个面上分别标上数字1，2，3，4，5，6．小明、小红、小刚三人从不同的角度去观察此正方体，观察结果问这个正方体各个面上的数字对面各是什么数字，错误的是（　　）
    分析：根据图形，4与1、6、3、5相邻，可以判断出4与2是相对面，3与1、2、4、5相邻，可以判断出3与6是相对面，然后得出1与5是相对面，然后即可进行选择．
    解答：解：根据图形的相邻面，∵4与1、6、3、5相邻，
    ∴4与2是相对面，
    ∵3与1、2、4、5相邻，
    ∴3与6是相对面，
    ∴1与5是相对面．
    故选A．
    点评：本题考查了正方体相对两个面上的文字，找出一个面的四个相邻面是判断其对面的关键，难度不大，关键是技巧．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

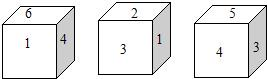
    2、如图所示，有一个正方体形的铁丝架，把它的侧棱中点I、J、K、L也用铁丝连上．
    （1）现在一个蚂蚁想沿着铁丝从A点爬到G点，问最近的路线一共有几条？并用字母把这些路线表示出来（用所经过的连接点字母表示，譬如蚂蚁从A点出发，经过I点L点，最后到达H点，这样的路线用AILH表示）．
    （2）蚂蚁是否可能从A点出发，沿着铁丝经过每一个连接点恰好一次，最后到达G点？如果可能，请找出一条这样的路线；如果不可能，说明为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于点O，训练时要求A、B两船始终关于O点对称．以O为原点，建立如图所示的坐标系，x轴、y轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线y=
    4x
    上运动，湖面风平浪静，双帆远影优美，训练中档教练船与A、B两船恰好在直线y=x上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示）．
    （1）发现C船时，A、B、C三船所在位置的坐标分别为A（
     
    ，
     
    ）、B（
     
    ，
     
    ）和C（
     
    ，
     
    ）；
    （2）发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系中，放置一个如图所示的直角三角形纸片AOB，已知OA=2，∠AOB=30度．D、E两点同时从原点O出发，D点以每秒
    		3
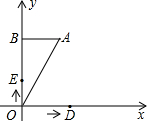    个单位长度的速度沿x轴正方向运动，E点以每秒1个单位精英家教网长度的速度沿y轴正方向运动，设D、E两点的运动时间为t秒．
    （1）点A的坐标为
     
    ，点B的坐标为
     
    ；
    （2）在点D、E的运动过程中，直线DE与直线OA垂直吗？请说明理由；
    （3）当时间t在什么范围时，直线DE与线段OA有公共点？
    （4）将直角三角形纸片AOB在直线DE下方的部分沿DE向上折叠，设折叠后重叠部分面积为S，请写出S与t的函数关系式，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    1、（1）如图，平面内两条互相
    垂直
    并且原点
    重合
    的
    数轴
    组成平面直角坐标系．其中，水平的数轴称为
    x轴
    或
    横轴
    ，习惯上取
    向右方向
    为正方向；竖直的数轴称为
    y轴
    或
    纵轴
    ，取
    向上方向
    为正方向；两坐标轴的交点叫做平面直角坐标系的
    原点
    ．直角坐标系所在的
    平面
    叫做坐标平面．

    （2）有了平面直角坐标系，平面内的点就可以用一个
    有序数对
    来表示．如果有序数对（a，b）表示坐标平面内的点A，那么有序数对（a，b）叫做
    A点的坐标
    ．其中，a叫做A点的
    横坐标
    ；b叫做A点的
    纵坐标
    ．
    （3）建立了平面直角坐标系以后，坐标平面就被
    两条坐标轴
    分成了Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分，如图所示，分别叫做
    第一象限
    、
    第二象限
    、
    第三象限
    、
    第四象限
    ．注意
    坐标轴上的点
    不属于任何象限．

    （4）坐标平面内，点所在的位置不同，它的坐标的符号特征如下：（请用“+”、“-”、“0”分别填写）

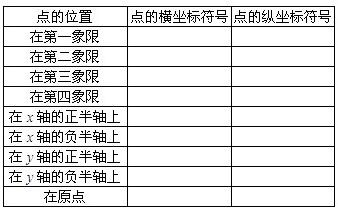
    查看答案和解析>>

    科目：初中数学 来源： 题型：

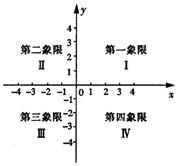
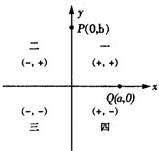
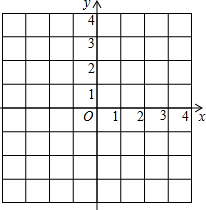    如图，平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分，以O为原点，建立如图所示的平面直角坐标系，x轴，y轴的正方向分别表示正东、正北方向，出租车只能沿街道（网格线）行驶，且从一个路口（格点）到另一个路口，必须选择最短路线，称最短路线的长度为两个街区之间的“出租车距离”．设图中每个小正方形方格的边长为1个单位．可以发现：
    从原点O到（2，-1）的“出租车距离”为3，最短路线有3条；
    从原点O到（2，2）的“出租车距离”为4，最短路线有6条．
    （1）①从原点O到（6，1）的“出租车距离”为
    7
    7
    ．最短路线有
    7
    7
    条；
    ②与原点O的“出租车距离”等于30的路口共有
    120
    120
    个．
    （2）①解释应用：从原点O到坐标（n，2）（n为大于2的整数）的路口A，有多少条最短路线？（请给出适当的说理或过程）
    ②解决问题：
    从坐标为（1，-2）的路口到坐标为（3，36）的路口，最短路线有
    780
    780
    条．

    查看答案和解析>>

    同步练习册答案