练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知⊙O半径为1，A、B在⊙O上，且，则AB所对的圆周角为__o.

    45或135 【解析】试题解析：如图所示， ∵OC⊥AB， ∴C为AB的中点,即 在Rt△AOC中,OA=1, 根据勾股定理得： 即OC=AC， ∴△AOC为等腰直角三角形， 同理 ∵∠AOB与∠ADB都对, ∵大角 则弦AB所对的圆周角为或 故答案为： 或
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    从正面观察如图所示的几何体，你所看到的几何体的形状是（ ）

    A. B. C. D.

    A 【解析】试题解析：从正面看，看到的图形是： 故选A.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：填空题

    方程（a-1）x|a|-3=0是关于x的一元一次方程，则a=_______．

    -1 【解析】由题意得： ，解得：a=-1， 故答案为：-1.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，在四边形ABCD中，∠B=90°，AD∥BC，BC=2AD，点E为边BC的中点．

    （1）求证：四边形AECD为平行四边形；

    （2）在CD边上取一点F，联结AF、 AC、 EF，设AC与EF交于点G，且∠EAF=∠CAD．

    求证：△AEC∽△ADF；

    （3）在（2）的条件下，当∠ECA=45°时．求： 的比值．

    （1）证明见解析;（2）证明见解析;（3）． 【解析】试题分析：（1）由E为BC中点，得到BC=2CE，再由BC=2AD，得到AD=CE，再由ADCE，利用一组对边平行且相等的四边形为平行四边形即可得证； （2）由四边形AECD为平行四边形，得到对角相等，再由已知角相等，利用两对角相等的三角形相似即可得证； （3）AD=BE=CE=a,由∠ECA=得到△ABC为等腰直角三角形，即AB=B...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型：解答题

    解方程：

    （1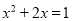）　　　　（2）

    （1）， ;（2）， . 【解析】试题分析：第小题用配方法，第小题用因式分解法. 试题解析： ， ， ， ， . （2）, , . ， .

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型：填空题

    如图，已知∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是__．（只需写一个条件，不添加辅助线和字母）

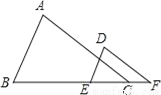
    AB∥DE（答案不唯一）． 【解析】在△ABC和△DEF中，已经有一个条件：∠A=∠D，根据三角形相似的判定方法中的：（1）有两个角对应相等的两个三角形相似；（2）有两边对应成比例，且夹角相等的两个三角形相似；可知：只需再添加“一对对应角相等”或“夹∠A、∠D的两边成比例”即可得到：△ABC∽△DEF，因此本题的答案不是唯一的，如添加的一个条件可以是：①∠B=∠DEF或②∠ACB=∠F或③A...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型：单选题

    为了考查某种小麦的长势，从中抽取了10株麦苗，测得苗高(单位:cm)为16，9，14,，11，12，10，16，8，17，19，则这组数据的中位数和极差分别是( )

    A. 13，11 B. 14，11 C. 12，11 D. 13，16

    A 【解析】试题解析：将数据从小到大排列为：8，9，10，11，12，14，16，16，17，19， 中位数为：13； 极差=19?8=11. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型：填空题

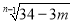    最简二次根式与是同类二次根式，则＝______________．

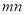    21 【解析】根据二次根式及同类二次根式的定义列出方程组即可求出答案. 【解析】 ∵最简二次根式与是同类二次根式， ∴ ， 解得， ， ∴ 故答案为：21.

    查看答案和解析>>

    科目：初中数学 来源：四川省自贡市2017－2018学年上学期九年级期末统一考试数学试卷 题型：解答题

    如图，点A的坐标为，点B的坐标为，点C的坐标为.

    ⑴请在平面直角坐标系中画出?ABC向上平移2个单位后的图形?A1B1C1.

    ⑵请在直角坐标系中画出?ABC绕点C逆时针旋转90°的三角形为?A′B′C′，直接写出点A′的坐标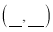 , 点B′的坐标.

    （1）图形见解析（2）-4，2；-1，3 【解析】试题分析：(1)、将A、B、C三点向上平移2个单位，然后顺次连接各点得到所求的三角形；(2)、根据旋转的性质找出各点旋转后所在的位置，然后顺次进行连接，根据坐标系得出点的坐标． 试题解析：(1)、如图所示： 如图所示：△就是所作的三角形； (2)、 如图所示就是所作的三角形； (﹣4，2)； (﹣1，3)． ...

    查看答案和解析>>

    同步练习册答案