
分析 (1)根据零指数幂、负整数指数幂、特殊角的三角函数值分别进行计算,然后相加即可得出答案;
(2)先分别求出不等式的解集,再根据大大取大得出不等式组的解集,然后画出数轴即可.
解答 解:(1)(2015)0×$\sqrt{8}$-($\frac{1}{2}$)-1-|3-$\sqrt{18}$|+2cos45°
=1×2$\sqrt{2}$-2-(3$\sqrt{2}$-3)+2×$\frac{\sqrt{2}}{2}$
=2$\sqrt{2}$-2-3$\sqrt{2}$+3+$\sqrt{2}$
=1;
(2)$\left\{\begin{array}{l}{4x-3>x①}\\{x+4<2x-1②}\end{array}\right.$,
解不等式①得x>1,
解不等式②得x>5,
则原不等式的解集为x>5;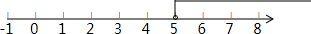
点评 此题考查了实数的运算和解一元一次不等式组,用到的知识点是零指数幂、负整数指数幂、特殊角的三角函数值以及在数轴上表示不等式的解集,熟练掌握它们的性质和定义是本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
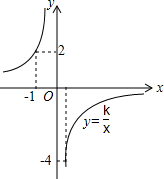 反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )
反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )| A. | -4≤x<0或0<x<2 | B. | x<-1或x≥$\frac{1}{2}$ | C. | -1<x≤$\frac{1}{2}$ | D. | -1<x<0或0<x≤$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
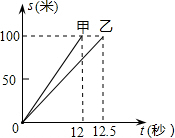 甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示.下列关于此次赛跑说法正确的是( )
甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示.下列关于此次赛跑说法正确的是( )| A. | 乙比甲跑的路程多 | B. | 这是一次100米赛跑 | ||
| C. | 甲乙同时到达终点 | D. | 甲的速度为8m/s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com