
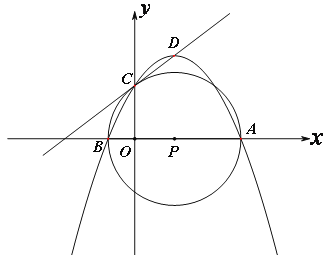
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c经过点A(4,0)、B(-1,0),与y轴交于点C,D为抛物线的顶点,过A、B、C 作⊙P.
x2+bx+c经过点A(4,0)、B(-1,0),与y轴交于点C,D为抛物线的顶点,过A、B、C 作⊙P.
(1)求b、c的值;
(2)求证:线段AB是⊙P的直径;
(3)连接AC,AD,在坐标平面内是否存在点Q,使得△CDA~△CPQ,若存在,求出点Q的坐标,若不存在,请说明理由。
【答案】(1) ![]() ;(2)证明见解析;(3)Q1(-
;(2)证明见解析;(3)Q1(-![]() ,-
,-![]() ),Q2(
),Q2(![]() ,
,![]() ).
).
【解析】
试题分析:(1)用待定系数法求出抛物线的系数b,c;
(2)先求出点C(0,2),再根据A(4,0)、B(-1,0),求出AC2,BC2,AB2,用勾股定理逆定理说明△ABC是直角三角形即可;
(3)先求出线段AC,AD,CD,CP,根据三角形相似得到比例式,再设出点Q的坐标建立方程求解.
试题解析:(1)∵抛物线y=-![]() x2+bx+c经过点A(4,0)、B(-1,0),
x2+bx+c经过点A(4,0)、B(-1,0),
∴ ,
,
∴![]()
(2)由(1)可知抛物线的解析式为:y=-![]() x2+
x2+![]() x+2,C(0,2),
x+2,C(0,2),
∵A(4,0)、B(-1,0),
∴BC2=OB2+OC2=1+4=5,AC2=OA2+OC2=16+4=20,AB2=25,
∴BC2+AC2=AB2,
∴∠ACB=90°,
∴线段AB是⊙P的直径;
(3)由(1)可知抛物线的解析式为:y=-![]() x2+
x2+![]() x+2,
x+2,
∴D(![]() ,
,![]() ),
),
∵A(4,0),C(0,2),
∴AC=2![]() ,AD=
,AD=![]() ,CD=
,CD=![]() ,
,
∵P(![]() ,0),
,0),
∴CP=![]() ,
,
∵△CDA∽△CPQ,
∴![]()
∴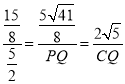 ,
,
∴PQ=![]() ,CQ=
,CQ=![]() ,
,
设点Q(m,n),
∴PQ=![]() =
=![]() ,
,
CQ=![]() =
=![]() ,
,
∴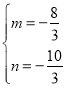 或
或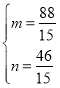 ,
,
∴Q1(-![]() ,-
,-![]() ),Q2(
),Q2(![]() ,
,![]() ).
).


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
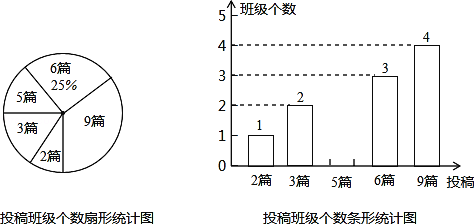
【题目】为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽新城市”的号召,我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的两个班级中,八,九年级各有两个班,校学生会准备从这四个中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com