
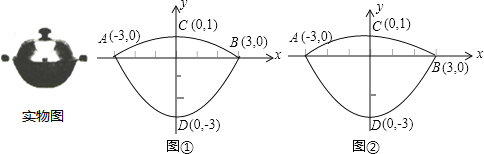
ЎҫМвДҝЎҝОТГЗіЈјыөДіҙІЛ№шәН№шёЗ¶јКЗЕЧОпПЯГжЈ¬ҫӯ№э№шРДәНёЗРДөДЧЭ¶ПГжКЗБҪ¶ЛЕЧОпПЯЧйәП¶шіЙөД·вұХНјРОЈ¬І»·БјтіЖОӘЎ°№шПЯЎұЈ¬№шҝЪЦұҫ¶ОӘ6dmЈ¬№шЙо3dmЈ¬№шёЗёЯ1dmЈЁ№шҝЪЦұҫ¶Ул№шёЗЦұҫ¶КУОӘПаН¬Ј©Ј¬ҪЁБўЦұҪЗЧшұкПөИзНјўЩЛщКҫЈЁНјўЪКЗұёУГНјЈ©Ј¬Из№ы°С№шЧЭ¶ПГжөДЕЧОпПЯјЗОӘC1Ј¬°С№шёЗЧЭ¶ПГжөДЕЧОпПЯјЗОӘC2Ј®
ЈЁ1Ј©ЗуC1әНC2өДҪвОцКҪЈ»
ЈЁ2Ј©Из№ыіҙІЛКұ№шөДЛ®О»ёЯ¶ИКЗ1dmЈ¬ЗуҙЛКұЛ®ГжөДЦұҫ¶Ј»
ЈЁ3Ј©Из№ыҪ«Т»ёцөЧГжЦұҫ¶ОӘ3dmЈ¬ёЯ¶ИОӘ3dmөДФІЦщРОЖчГу·ЕИліҙІЛ№шДЪХфКіОпЈ¬№шёЗДЬ·сХэіЈёЗЙПЈҝЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©ЕЧОпПЯC1Јәy=![]() x2©Ғ3ЈЁ©Ғ3ЎЬxЎЬ3Ј©Ј¬ЕЧОпПЯC2Јәy=©Ғ
x2©Ғ3ЈЁ©Ғ3ЎЬxЎЬ3Ј©Ј¬ЕЧОпПЯC2Јәy=©Ғ![]() x2+1ЈЁ©Ғ3ЎЬxЎЬ3Ј©Ј»ЈЁ2Ј©2
x2+1ЈЁ©Ғ3ЎЬxЎЬ3Ј©Ј»ЈЁ2Ј©2![]() dmЈ»ЈЁ3Ј©№шёЗДЬХэіЈёЗЙПЈ¬АнУЙјыҪвОц.
dmЈ»ЈЁ3Ј©№шёЗДЬХэіЈёЗЙПЈ¬АнУЙјыҪвОц.
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©ТСЦӘAЎўBЎўCЎўDЛДөгЧшұкЈ¬АыУГҙэ¶ЁПөКэ·ЁјҙҝЙИ·¶ЁБҪәҜКэөДҪвОцКҪЈ»
ЈЁ2Ј©іҙІЛ№шАпөДЛ®О»ёЯ¶ИОӘ1dmјҙy=-2Ј¬БР·ҪіМЗуөГxөДЦөјҙҝЙөГҙр°ёЈ»
ЈЁ3Ј©өЧГжЦұҫ¶ОӘ3dmЎўёЯ¶ИОӘ3dmФІЦщРОЖчГуДЬ·с·ЕИл№шДЪЈ¬РиЕР¶Пөұx=![]() КұЈ¬C1әНC2ЦРөДyЦөөДІоУл3ұИҪПҙуРЎЈ¬ҙУ¶шҝЙөГҙр°ёЈ®
КұЈ¬C1әНC2ЦРөДyЦөөДІоУл3ұИҪПҙуРЎЈ¬ҙУ¶шҝЙөГҙр°ёЈ®
ҪвЈәЈЁ1Ј©УЙУЪЕЧОпПЯC1ЎўC2¶ј№эөгAЈЁ©Ғ3Ј¬0Ј©ЎўBЈЁ3Ј¬0Ј©Ј¬ҝЙЙиЛьГЗөДҪвОцКҪОӘЈәy=aЈЁx©Ғ3Ј©ЈЁx+3Ј©Ј»
ЕЧОпПЯC1»№ҫӯ№эDЈЁ0Ј¬©Ғ3Ј©Ј¬
ФтУРЈә©Ғ3=aЈЁ0©Ғ3Ј©ЈЁ0+3Ј©Ј¬ҪвөГЈәa=![]()
јҙЈәЕЧОпПЯC1Јәy=![]() x2©Ғ3ЈЁ©Ғ3ЎЬxЎЬ3Ј©Ј»
x2©Ғ3ЈЁ©Ғ3ЎЬxЎЬ3Ј©Ј»
ЕЧОпПЯC2»№ҫӯ№эCЈЁ0Ј¬1Ј©Ј¬
ФтУРЈә1=aЈЁ0©Ғ3Ј©ЈЁ0+3Ј©Ј¬ҪвөГЈәa=©Ғ![]()
јҙЈәЕЧОпПЯC2Јәy=©Ғ![]() x2+1ЈЁ©Ғ3ЎЬxЎЬ3Ј©Ј®
x2+1ЈЁ©Ғ3ЎЬxЎЬ3Ј©Ј®
ЈЁ2Ј©өұіҙІЛ№шАпөДЛ®О»ёЯ¶ИОӘ1dmКұЈ¬y=©Ғ2Ј¬јҙ![]() x2©Ғ3=©Ғ2Ј¬
x2©Ғ3=©Ғ2Ј¬
ҪвөГЈәx=ЎА![]() Ј¬
Ј¬
ЎаҙЛКұЛ®ГжөДЦұҫ¶ОӘ2![]() dmЈ®
dmЈ®
ЈЁ3Ј©№шёЗДЬХэіЈёЗЙПЈ¬АнУЙИзПВЈә
өұx=![]() КұЈ¬ЕЧОпПЯC1Јәy=
КұЈ¬ЕЧОпПЯC1Јәy=![]() ЎБЈЁ
ЎБЈЁ![]() Ј©2©Ғ3=©Ғ
Ј©2©Ғ3=©Ғ![]() Ј¬ЕЧОпПЯC2Јәy=©Ғ
Ј¬ЕЧОпПЯC2Јәy=©Ғ![]() ЎБЈЁ
ЎБЈЁ![]() Ј©2+1=
Ј©2+1=![]() Ј¬
Ј¬
¶ш![]() ©ҒЈЁ©Ғ
©ҒЈЁ©Ғ![]() Ј©=3Ј¬
Ј©=3Ј¬
Ўа№шёЗДЬХэіЈёЗЙП.


 ҝЪЛгРЎЧҙФӘҝЪЛгЛЩЛгМмМмБ·ПөБРҙр°ё
ҝЪЛгРЎЧҙФӘҝЪЛгЛЩЛгМмМмБ·ПөБРҙр°ё МмМмБ·ҝЪЛгПөБРҙр°ё
МмМмБ·ҝЪЛгПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ°ЛДк2°аЧйЦҜБЛТ»ҙОҫӯөдЛР¶БұИИьЈ¬јЧТТБҪЧйёч10ИЛөДұИИьіЙјЁИзПВұнЈЁ10 ·ЦЦЖЈ©Јә
јЧ | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
ТТ | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
ўЩјЧЧйКэҫЭөДЦРО»КэКЗ Ј¬ ТТЧйКэҫЭөДЦЪКэКЗЈ»
ўЪјЖЛгТТЧйКэҫЭөДЖҪҫщКэ·ҪІоЈ»
ўЫТСЦӘјЧЧйКэҫЭөД·ҪІоКЗ1.4·Ц2 Ј¬ ФтіЙјЁҪПОӘХыЖлөДКЗ Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈЁa-4Ј©ЈЁa-2Ј©=3Ј¬ФтЈЁa-4Ј©2+ЈЁa-2Ј©2өДЦөОӘ__________Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ№ШУЪ¶аПоКҪx2Ј«y2Јӯ1өДПоКэј°ҙОКэЈ¬ПВБРЛө·ЁХэИ·өДКЗЈЁЎЎЎЎЈ©
A.ПоКэКЗ2Ј¬ҙОКэКЗ2B.ПоКэКЗ2Ј¬ҙОКэКЗ4
C.ПоКэКЗ3Ј¬ҙОКэКЗ2D.ПоКэКЗ3Ј¬ҙОКэКЗ4
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝУГЛДЙбОеИЛ·Ё°ҙТӘЗу¶Ф0.05802·ЦұрИЎҪьЛЖЦөөГөҪПВБРҪб№ыЈ¬ЖдЦРҙнОуөДКЗЈЁЎЎЎЎЈ©
A.0.1ЈЁҫ«И·өҪ0.1Ј©B.0.06ЈЁҫ«И·өҪ°Щ·ЦО»Ј©
C.0.058ЈЁҫ«И·өҪЗ§·ЦО»Ј©D.0.058ЈЁҫ«И·өҪ0.0001Ј©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј,ТСЦӘЎчABC,ADЖҪ·ЦЎПBACҪ»BCУЪөгD,BCөДЦРөгОӘM,MEЎОAD,Ҫ»BAөДСУіӨПЯУЪөгE,Ҫ»ACУЪөгF.ЗуЦӨ: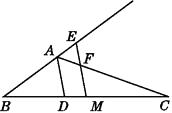
ЈЁ1Ј©AE=AF;
ЈЁ2Ј©BE= ![]() (AB+AC).
(AB+AC).
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘABКЗ°лҫ¶ОӘ1өДФІOЦұҫ¶Ј¬CКЗФІЙПТ»өгЈ¬DКЗBCСУіӨПЯЙПТ»өгЈ¬№эөгDөДЦұПЯҪ»ACУЪEөгЈ¬ЗТЎчAEFОӘөИұЯИэҪЗРО
ЈЁ1Ј©ЗуЦӨЈәЎчDFBКЗөИСьИэҪЗРОЈ»
ЈЁ2Ј©ИфDA=![]() AFЈ¬ЗуЦӨЈәCFЎНABЈ®
AFЈ¬ЗуЦӨЈәCFЎНABЈ®

Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com