
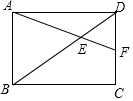
 如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则$\frac{CF}{CD}$等于( )
如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于F,则$\frac{CF}{CD}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
分析 根据勾股定理求出BD,得到DE的长,根据相似三角形的性质得到比例式,代入计算即可求出DF的长,求出CF,计算即可.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,又AB=$\sqrt{3}$,BC=$\sqrt{6}$,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=3,
∵BE=1.8,
∴DE=3-1.8=1.2,
∵AB∥CD,
∴$\frac{DF}{AB}$=$\frac{DE}{BE}$,即$\frac{DF}{\sqrt{3}}$=$\frac{1.2}{1.8}$,
解得,DF=$\frac{2\sqrt{3}}{3}$,
则CF=CD-DF=$\frac{\sqrt{3}}{3}$,
∴$\frac{CF}{CD}$=$\frac{\frac{\sqrt{3}}{3}}{\sqrt{3}}$=$\frac{1}{3}$,
故选A.
点评 本题考查的是矩形的性质、相似三角形的判定和性质,掌握矩形的性质定理和相似三角形的判定定理、性质定理是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
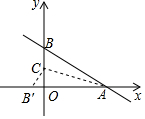 如图,在平面直角坐标系中,已知直线y=-$\frac{3}{4}$x+3与x轴,y轴分别交于A、B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
如图,在平面直角坐标系中,已知直线y=-$\frac{3}{4}$x+3与x轴,y轴分别交于A、B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )| A. | (0,$\frac{3}{4}$) | B. | (0,$\frac{4}{3}$) | C. | (0,3) | D. | (0,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx-3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=-1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).
如图,抛物线y=ax2+bx-3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=-1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
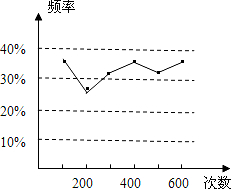 甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则 符合这一结果的实验可能是( )
甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则 符合这一结果的实验可能是( )| A. | 掷一枚正六面体的骰子,出现6点的概率 | |
| B. | 掷一枚硬币,出现正面朝上的概率 | |
| C. | 任意写出一个整数,能被2整除的概率 | |
| D. | 一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+1)2-2 | B. | y=(x-5)2-2 | C. | y=(x-5)2-12 | D. | y=(x+1)2-12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{10}{3}$ | B. | 3.1415926 | C. | $\root{3}{8}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象分布在第一、三象限 | B. | 它的图象与直线y=-x无交点 | ||
| C. | 当x>0时,y的值随x的增大而增大 | D. | 当x<0时,y的值随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com