
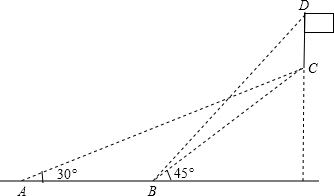
分析 设EC=x,则在Rt△BCE中,BC=EC=x;在Rt△ACE中,tan30°=$\frac{CE}{AE}$=$\frac{x}{100+x}$=$\frac{\sqrt{3}}{3}$,利用关系式AC=CD列方程求出x,从而求得BE=CE=50$\sqrt{3}$+50,在Rt△BED中,DE=tan48°•BE=1.11×(50$\sqrt{3}$+50)≈151.5,旗杆高CD=DE-EC可以求出.
解答 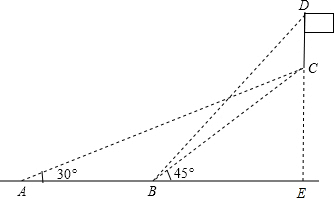 解:设EC=x(米),
解:设EC=x(米),
在Rt△BCE中,∠EBC=45°,
∴BE=x;
在Rt△ACE中,∠A=30°,
∴tan30°=$\frac{CE}{AE}$=$\frac{x}{100+x}$=$\frac{\sqrt{3}}{3}$;
∴3x=100$\sqrt{3}$+$\sqrt{3}$x,
解得x=50$\sqrt{3}$+50,
∴BE=CE=50$\sqrt{3}$+50,
在Rt△BED中,∠DBE=48°,
∴DE=tan48°•BE=1.11×(50$\sqrt{3}$+50)≈151.5,
∴DC=DE-CE=151.5-136.5=15.0(米).
答:旗杆的高度约为15.0米
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识表示出相关线段的长度,难度一般.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
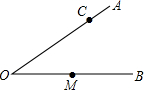 如图,∠AOB=30°,点M在OB上,且OM=5cm,以M为圆心,r为半径画圆.
如图,∠AOB=30°,点M在OB上,且OM=5cm,以M为圆心,r为半径画圆.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 多边形的边数 | 7 | 17 | 20 | 25 |
| 内角和 | 5×180° | 15×180° | 18×180° | 23×180° |
| 外角和 | 360° | 360° | 360° | 360° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
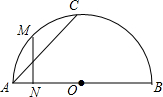 如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )
如图,AB是半圆O的直径,C是半圆圆周上一点,M是弧AC的中点,MN⊥AB于N,则有( )| A. | MN=$\frac{1}{2}$AC | B. | MN=$\frac{\sqrt{2}}{2}$AC | C. | MN=$\frac{3}{5}$AC | D. | MN=$\frac{\sqrt{3}}{3}$AC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com