
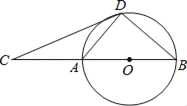
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若BC=6,tan∠CDA=![]() ,求CD的长.
,求CD的长.
【答案】(1)证明见解析;(2)4.
【解析】
(1)连接OD,如图,先证明∠CDA=∠ODB,再根据圆周角定理得∠ADO+∠ODB=90°,则∠ADO+∠CDA=90°,即∠CDO=90°,于是根据切线的判定定理即可得到结论;
(2)由于∠CDA=∠ODB,则tan∠CDA=tan∠ABD=![]() ,根据正切的定义得到tan∠ABD=
,根据正切的定义得到tan∠ABD=![]() ,接着证明△CAD∽△CDB,由相似的性质得
,接着证明△CAD∽△CDB,由相似的性质得![]() ,然后根据比例的性质可计算出CD的长.
,然后根据比例的性质可计算出CD的长.
详(1)证明:连接OD,如图,
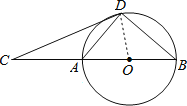
∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
∵AB是⊙O的直径,
∴∠ADB=90°,即∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∴CD是⊙O的切线;
(2)∵∠CDA=∠ODB,
∴tan∠CDA=tan∠ABD=![]() ,
,
在Rt△ABD中,tan∠ABD=![]() ,
,
∵∠DAC=∠BDC,∠CDA=∠CBD,
∴△CAD∽△CDB,
∴![]() ,
,
∴CD=![]() ×6=4.
×6=4.


科目:初中数学 来源: 题型:
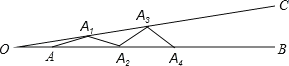
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )
A. 10B. 9C. 8D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A、C、F在一条直线上( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①位似图形一定是相似图形②相似图形一定是位似图形
③位似图形对应顶点的连线相交于一点④位似图形的对应边互相平行.
其中正确的有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
由于雾霾天气频发,市场上防护口罩出现热销.某药店准备购进一批口罩,已知1个A型口罩和3个B型口罩共需26元;3个A型口罩和2个B型口罩共需29元.
⑴ 求一个A型口罩和一个B型口罩的售价各是多少元?
⑵ 药店准备购进这两种型号的口罩共50个,其中A型口罩数量不少于35个,且不多于B型口罩的3倍,有哪几种购买方案,哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,求AA′的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com