

分析 (1)利用相似三角形的性质求出每个纸条的长;
(2)将(1)中相关数据相加,易得纸片的宽度,从而计算出正方形的边长,从而计算面积即可.
解答 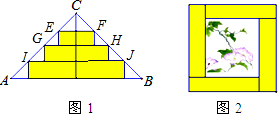 解:(1)如图1,∵△ABC是等腰直角三角形,AC=BC=40cm,CD是斜边AB上的高,
解:(1)如图1,∵△ABC是等腰直角三角形,AC=BC=40cm,CD是斜边AB上的高,
∴AB=40$\sqrt{2}$cm,CD是斜边上的中线,
∴CD=$\frac{1}{2}$AB=20$\sqrt{2}$cm,
于是纸条的宽度为:$\frac{20\sqrt{2}}{4}$=5$\sqrt{2}$(cm),
∵$\frac{EF}{AB}$=$\frac{1}{4}$,
∴EF=$\frac{1}{4}$AB=10$\sqrt{2}$cm.
同理,GH=20$\sqrt{2}$cm,
IJ=30$\sqrt{2}$cm,
∴3张长方形纸条的长度分别为:10$\sqrt{2}$cm,20$\sqrt{2}$cn,30$\sqrt{2}$cm;
(2)由(1)知,3张长方形纸条的总长度为60$\sqrt{2}$cm.
如图2,图画的正方形的边长为:$\frac{60\sqrt{2}}{4}$-5$\sqrt{2}$=10$\sqrt{2}$(cm),
∴面积为(10$\sqrt{2}$)2=200(cm2)
答:如图(b) 正方形美术作品的面积最大不能超过200cm2.
点评 此题考查了相似三角形的应用,不仅要计算出纸条的长度,还要计算出宽度,要仔细观察图形,寻找隐含条件.


科目:初中数学 来源: 题型:选择题
 如图,将边长为5cm的等边△ABC沿边BC向右平移4cm得到△A′B′C′,则四边形AA′C′B的周长为( )
如图,将边长为5cm的等边△ABC沿边BC向右平移4cm得到△A′B′C′,则四边形AA′C′B的周长为( )| A. | 22cm | B. | 23cm | C. | 24cm | D. | 25cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 实数和数轴上的点一一对应 | |
| C. | 平行于同一条直线的两条直线平行 | |
| D. | 三角形的一个外角大于任何一个和它不相邻的内角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ②③ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com