
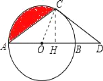
【题目】(12分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3, ![]() 的长为π.
的长为π.
(1)直线CD与⊙O相切吗?说明理由。
(2)求阴影部分的面积.

【答案】(1)相切(2)![]()
【解析】试题分析:(1)、首先连接OC,根据弧的长度得出∠BOC=60°,然后根据等腰三角形的性质得出∠D=∠CAD=30°,从而得出∠OCD=90°,即得出切线;(2)、根据题意得出∠AOC=120°,然后根据阴影部分的面积=扇形AOC的面积减去△AOC的面积得出答案.
试题解析:(1)相切。
理由:连接OC,设∠BOC的度数为n°,则![]() =π,
=π,
解得n=60°,
∴∠A=![]() ∠BOC=30°,
∠BOC=30°,
∵AC=CD,
∴∠A=∠D=30°,
∴∠OCD=180°﹣∠BOC﹣∠D=180°﹣30°﹣60°=90°,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:作CH⊥OB于H,则CH=OCsin60°=3×![]() =
=![]() ,
,
∵∠BOC=60°,
∴∠AOC=120°,
∴S阴影=S扇形OAC﹣S△OAC=![]() ﹣
﹣![]() ×3×
×3×![]() =
=![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥DF交AB于点E,连接EG、EF. 
(1)求证:BG=CF;
(2)求证:EG=EF;
(3)请你判断BE+CF与EF的大小关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.

(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2 , 请画出△A2B2C2;
(3)若点O的坐标为(0,0),点B的坐标为(2,3);写出△A1B1C1与△A2B2C2的对称中心的坐标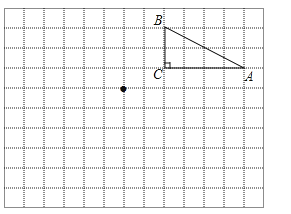
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旧车交易市场有一辆原价为12万元的轿车,已使用3年,如果第一年的折旧率为20%,后其折旧率有所变化,现知第三年末这辆轿车值7.776万元.假设这辆车第二、第三年平均每年的折旧率都相同,那么这辆车第二、第三年平均每年的折旧率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com