
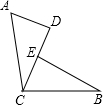
 如图,已知∠ACB=90°,且AC=BC,AD⊥CD,BE⊥CD,垂足分别为D、E,求证:CD=BE.
如图,已知∠ACB=90°,且AC=BC,AD⊥CD,BE⊥CD,垂足分别为D、E,求证:CD=BE.  口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
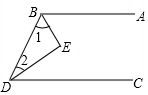 (1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.
(1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
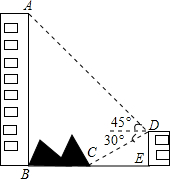 如图,大楼沿右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同-水平直线上.己知AB=80m,DE=10m,求障碍物B、C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼沿右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同-水平直线上.己知AB=80m,DE=10m,求障碍物B、C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com