
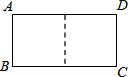
 �ڱ߲���ȵľ���ֽƬ����ȥһ�����������Σ�����һ���ı��Σ���Ϊ��һ�β����������µľ���ֽƬ���ټ�ȥһ�����������Σ�����һ���ı��Σ���Ϊ�ڶ��β��������������ƣ�����n�����µ��ı����������Σ����ԭ����Ϊn���Σ���ͼ������ABCD�У���AB=1��BC=2�������ABCDΪ1���Σ�
�ڱ߲���ȵľ���ֽƬ����ȥһ�����������Σ�����һ���ı��Σ���Ϊ��һ�β����������µľ���ֽƬ���ټ�ȥһ�����������Σ�����һ���ı��Σ���Ϊ�ڶ��β��������������ƣ�����n�����µ��ı����������Σ����ԭ����Ϊn���Σ���ͼ������ABCD�У���AB=1��BC=2�������ABCDΪ1���Σ����� ��1����һ����������α߳�Ϊ2���ڶ�����������α߳�Ϊ1�����µ������α߳�Ϊ1�������ڱ߳��ֱ�Ϊ2��3�ľ�����2���Σ�
��һ����������α߳�Ϊ3���ڶ����͵�������������α߳���Ϊ1�����µ������α߳�Ϊ1�������ڱ߳��ֱ�Ϊ3��4�ľ�����3���Σ�
��2��a���ĸ�ֵ����a=4ʱ���������������α߳���Ϊ1�����µ������α߳�Ϊ1��
��a=$\frac{5}{2}$ʱ����һ���͵ڶ��������α߳���Ϊ1�������������α߳�Ϊ$\frac{1}{2}$�����µ������α߳�Ϊ$\frac{1}{2}$��
��a=$\frac{4}{3}$ʱ����һ�������α߳�Ϊ1���ڶ����͵����������α߳���Ϊ$\frac{1}{3}$�����µ������α߳�Ϊ$\frac{1}{3}$��
��a=$\frac{5}{3}$ʱ����һ�������α߳�Ϊ1���ڶ��������α߳�Ϊ$\frac{2}{3}$�������������α߳�Ϊ$\frac{1}{3}$�����µ������α߳�Ϊ$\frac{1}{3}$��
��3���ȼ���a=21r��ǰ��������α߳���Ϊ4r�����ĸ������α߳���Ϊr�����Ծ���ABCD��8���Σ�
��� �⣺��1����Ϊ��2�ף�3�ף�
��ͼ���£�
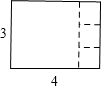
��2����ͼ���£�
��3����a=5b+r��b=4r��
��a=5��4r+r=21r��
��ͼ���£�
�����ABCD��8����
���� ������һ���ı��ε��Ķ������⣬������ѧ�����Ķ���������������һ���µĶ��壬���˶������Ⲣ������⣬������Ĺؼ������ص���䣺��������������Σ���������µ�Ҳ��һ�������Σ���n�������Σ�����n-1���Σ����������ν�ϵ�˼�룬ʹ���������������������廯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -5 | C�� | -3 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\sqrt{3}$ | C�� | -2 | D�� | ��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com