
【题目】小强在某超市同时购买A,B两种商品共三次,仅有第一次超市将A,B两种商品同时按![]() 折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
A商品的数量(个) | B商品的数量(个) | 购买总费用(元) | |
第一次购买 | 8 | 6 | 930 |
第二次购买 | 6 | 5 | 980 |
第三次购买 | 3 | 8 | 1040 |
(1)求 A,B商品的标价;
(2)求![]() 的值.
的值.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析表达式为,且
的解析表达式为,且![]() 与
与![]() 轴交于点D,直线
轴交于点D,直线![]() 经过点A,B,直线
经过点A,B,直线![]() ,
,![]() 交于点C.
交于点C.
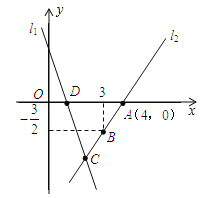
(1)求直线![]() 的解析式;
的解析式;
(2)求△ADC的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平移和翻折是初中阶段研究的两种重要的图形运动。
(平移运动)
(1)把笔尖放在数轴的原点,然后沿数轴向左移动 5 个单位长度,再向右移动3 个单位长度,这时笔尖的位置表示什么数?用算式可以将以上过程及结果表示为_____。
(2)把笔尖放在数轴的原点,第 1 次向左跳 2 个单位,紧接着第 2 次向右跳 4个单位,第 3 次向左跳 6 个单位,第 4 次向右跳 8 个单位,……依次规律跳,当它跳了 2019 次时,这时笔尖的位置表示的数是_____。

(翻折运动)
已知纸面上有一数轴,折叠纸面。

(3)若 1 表示的点与﹣1 表示的点重合,则﹣9 表示的点与_____表示的点重合。
(4)若 1 表示的点与﹣5 表示的点重合,回答以下问题:
① 3 表示的点与_____表示的点重合;
② 若数轴上 A,B 两点之间的距离为 2020(A 在 B 的左侧,且折痕与①折痕相同),且 A、B 两点经折叠后重合,则 A 点表示的数是 _____,B 点表示的数是_____;
(5)若数轴上折叠重合的两点表示的数分别为 a,b,那么数 c 表示的点与数_______表示的点也重合。(用含有 a,b,c 的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
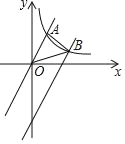
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,∠ACB=90°,AB=![]() ,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
(1)若CM=![]() ,则AM= ;
,则AM= ;
(2)如图①,若点E是BM的中点,求证:MN=AM;
(3)如图②,若点N落在BA的延长线上,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD 中,边CD 5 ,对角线 AC 8 , DB 6.
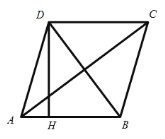
(1)求证:四边形 ABCD 是菱形;
(2)过点 D 作 DH AB 于点 H ,若点 P 是线段 AC 上的一个动点,求 PH PB 的最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织初一师生春游,如果单独租用45座客车若干辆,刚好坐满;如果单独租用60座客车,可少租1辆,且余15个座位.
(1)求参加春游的人数;
(2)已知租用45座的客车日租金为每辆车250元, 60座的客车日租金为每辆300元,问租哪种客车更合算?省多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com