
ЎҫМвДҝЎҝЈЁФД¶БАнҪвЈ©ИфКэЦбЙПБҪөг![]() Ј¬
Ј¬![]() ЛщұнКҫөДКэ·ЦұрОӘ
ЛщұнКҫөДКэ·ЦұрОӘ![]() әН
әН![]() Ј¬ФтУРЈә
Ј¬ФтУРЈә
ўЩ![]() Ј¬
Ј¬![]() БҪөгөДЦРөгұнКҫөДКэОӘ
БҪөгөДЦРөгұнКҫөДКэОӘ![]() Ј»
Ј»
ўЪ![]() Ј¬
Ј¬![]() БҪөгЦ®јдөДҫаАл
БҪөгЦ®јдөДҫаАл![]() Ј»Иф
Ј»Иф![]() Ј¬ФтҝЙјт»ҜОӘ
Ј¬ФтҝЙјт»ҜОӘ![]() Ј®
Ј®
ЈЁҪвҫцОКМвЈ©КэЦбЙПБҪөг![]() Ј¬
Ј¬![]() ЛщұнКҫөДКэ·ЦұрОӘ
ЛщұнКҫөДКэ·ЦұрОӘ![]() әН
әН![]() Ј¬ЗТВъЧг
Ј¬ЗТВъЧг![]() Ј®
Ј®
ЈЁ1Ј©Зуіц![]() Ј¬
Ј¬![]() БҪөгөДЦРөг
БҪөгөДЦРөг![]() ұнКҫөДКэЈ»
ұнКҫөДКэЈ»
ЈЁ2Ј©өг![]() ҙУФӯөг
ҙУФӯөг![]() өгіц·ўПтУТФЛ¶ҜЈ¬ҫӯ№э
өгіц·ўПтУТФЛ¶ҜЈ¬ҫӯ№э![]() Гләуөг
Гләуөг![]() өҪ
өҪ![]() өгөДҫаАлКЗөг
өгөДҫаАлКЗөг![]() өҪ
өҪ![]() өгҫаАлөД
өгҫаАлөД![]() ұ¶Ј¬Зуөг
ұ¶Ј¬Зуөг![]() өДФЛ¶ҜЛЩ¶ИКЗГҝГл¶аЙЩёцөҘО»іӨ¶ИЈҝ
өДФЛ¶ҜЛЩ¶ИКЗГҝГл¶аЙЩёцөҘО»іӨ¶ИЈҝ
ЈЁКэС§ЛјҝјЈ©
ЈЁ3Ј©өг![]() ТФГҝГл
ТФГҝГл![]() ёцөҘО»өДЛЩ¶ИҙУФӯөг
ёцөҘО»өДЛЩ¶ИҙУФӯөг![]() іц·ўПтУТФЛ¶ҜЈ¬Н¬КұЈ¬өг
іц·ўПтУТФЛ¶ҜЈ¬Н¬КұЈ¬өг![]() ҙУөг
ҙУөг![]() іц·ўТФГҝГл
іц·ўТФГҝГл![]() ёцөҘО»өДЛЩ¶ИПтЧуФЛ¶ҜЈ¬өг
ёцөҘО»өДЛЩ¶ИПтЧуФЛ¶ҜЈ¬өг![]() ҙУөг
ҙУөг![]() іц·ўЈ¬ТФГҝГл
іц·ўЈ¬ТФГҝГл![]() ёцөҘО»өДЛЩ¶ИПтУТФЛ¶ҜЈ¬
ёцөҘО»өДЛЩ¶ИПтУТФЛ¶ҜЈ¬![]() Ўў
Ўў![]() ·ЦұрОӘ
·ЦұрОӘ![]() Ўў
Ўў![]() өДЦРөгЈ®ЛјҝјЈәФЪФЛ¶Ҝ№эіМЦРЈ¬
өДЦРөгЈ®ЛјҝјЈәФЪФЛ¶Ҝ№эіМЦРЈ¬![]() өДЦөКЗ·с·ўЙъұд»ҜЈҝИз№ыГ»УРұд»ҜЈ¬ЗлЗуіцХвёцЦөЈ»Из№ы·ўЙъұд»ҜЈ¬ЗлЛөГчАнУЙЈ®
өДЦөКЗ·с·ўЙъұд»ҜЈҝИз№ыГ»УРұд»ҜЈ¬ЗлЗуіцХвёцЦөЈ»Из№ы·ўЙъұд»ҜЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©3Ј»ЈЁ2Ј©өгDөДФЛ¶ҜЛЩ¶ИКЗГҝГл![]() ёцөҘО»іӨ¶ИЈ¬»тГҝГл4ёцөҘО»іӨ¶ИЈ»ЈЁ3Ј©І»ұдЈ¬
ёцөҘО»іӨ¶ИЈ¬»тГҝГл4ёцөҘО»іӨ¶ИЈ»ЈЁ3Ј©І»ұдЈ¬![]()
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭ·ЗёәКэөДРФЦКәНЦРөгЧшұкөДЗу·ЁјҙҝЙөГөҪҪбВЫЈ»
ЈЁ2Ј©ЙиөгDөДФЛ¶ҜЛЩ¶ИОӘvЈ¬ўЩөұөгDФЛ¶ҜөҪөгCЧуұЯКұЈ¬ўЪөұөгDФЛ¶ҜөҪөгCУТұЯКұЈ¬ёщҫЭМвТвБР·ҪіМјҙҝЙөГөҪҪбВЫЈ»
ЈЁ3Ј©ЙиФЛ¶ҜКұјдОӘtЈ¬ФтөгE¶ФУҰөДКэКЗtЈ¬өгM¶ФУҰөДКэКЗ27tЈ¬өгN¶ФУҰөДКэКЗ8Ј«10tЈ®ёщҫЭМвТвЗуөГPөг¶ФУҰөДКэКЗ![]() ЈҪ13tЈ¬Qөг¶ФУҰөДКэКЗ
ЈҪ13tЈ¬Qөг¶ФУҰөДКэКЗ![]() ЈҪ4Ј«5tЈ¬УЪКЗЗуөГҪбВЫЈ®
ЈҪ4Ј«5tЈ¬УЪКЗЗуөГҪбВЫЈ®
ҪвЈәЈЁ1Ј©ЎЯ|a+2|+ЈЁb-8Ј©2020=0
Ўаa=-2Ј¬b=8Ј¬
ЎаAЎўBБҪөгөДЦРөгCұнКҫөДКэКЗЈә![]() ЈҪ3Ј»
ЈҪ3Ј»
ЈЁ2Ј©ЙиөгDөДФЛ¶ҜЛЩ¶ИОӘvЈ¬
ўЩөұөгDФЛ¶ҜөҪөгCЧуұЯКұЈәУЙМвТвЈ¬УР2v-ЈЁ-2Ј©=2ЈЁ3-2vЈ©Ј¬
ҪвЦ®өГvЈҪ![]()
ўЪөұөгDФЛ¶ҜөҪөгCУТұЯКұЈәУЙМвТвЈ¬УР2v-ЈЁ-2Ј©=2ЈЁ2v-3Ј©Ј¬
ҪвЦ®өГv=4Ј»
ЎаөгDөДФЛ¶ҜЛЩ¶ИКЗГҝГл![]() ёцөҘО»іӨ¶ИЈ¬»тГҝГл4ёцөҘО»іӨ¶ИЈ»
ёцөҘО»іӨ¶ИЈ¬»тГҝГл4ёцөҘО»іӨ¶ИЈ»
ЈЁ3Ј©ЙиФЛ¶ҜКұјдОӘtЈ¬ФтөгE¶ФУҰөДКэКЗtЈ¬өгM¶ФУҰөДКэКЗ-2-7tЈ¬өгN¶ФУҰөДКэКЗ8+10tЈ®
ЎЯPКЗMEөДЦРөгЈ¬
ЎаPөг¶ФУҰөДКэКЗ![]() ЈҪ13tЈ¬
ЈҪ13tЈ¬
УЦЎЯQКЗONөДЦРөгЈ¬
ЎаQөг¶ФУҰөДКэКЗ![]() ЈҪ4+5tЈ¬
ЈҪ4+5tЈ¬
ЎаMN=ЈЁ8+10tЈ©-ЈЁ-2-7tЈ©=10+17tЈ¬OE=t
PQ=ЈЁ4+5tЈ©-ЈЁ-1-3tЈ©=5+8tЈ¬
Ўа![]()
Ўа![]() өДЦөІ»ұдЈ¬өИУЪ2Ј®
өДЦөІ»ұдЈ¬өИУЪ2Ј®


 УўІЕөгҪтПөБРҙр°ё
УўІЕөгҪтПөБРҙр°ё әм№ыЧУИэј¶ІвКФҫнПөБРҙр°ё
әм№ыЧУИэј¶ІвКФҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
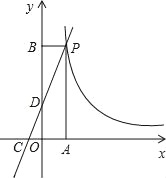
ЎҫМвДҝЎҝИзНјЈ¬Т»ҙОәҜКэy=kx+2өДНјПуУл·ҙұИАэәҜКэy=![]() өДНјПуФЪөЪТ»ПуПЮөДҪ»өгОӘPЈ¬PAЎНxЦбУЪөгAЈ¬PBЎНyЦбУЪөгBЈ¬әҜКэy=kx+2өДНјПу·ЦұрҪ»xЦбЈ¬yЦбУЪөгCЈ¬DЈ¬ТСЦӘЎчOCDөДГж»эSЎчOCD=1Ј¬
өДНјПуФЪөЪТ»ПуПЮөДҪ»өгОӘPЈ¬PAЎНxЦбУЪөгAЈ¬PBЎНyЦбУЪөгBЈ¬әҜКэy=kx+2өДНјПу·ЦұрҪ»xЦбЈ¬yЦбУЪөгCЈ¬DЈ¬ТСЦӘЎчOCDөДГж»эSЎчOCD=1Ј¬![]() =
=![]()
ЈЁ1Ј©ЗуөгDөДЧшұкЈ»
ЈЁ2Ј©ЗуkЈ¬mөДЦөЈ»
ЈЁ3Ј©РҙіцөұxЈҫ0КұЈ¬К№Т»ҙОәҜКэy=kx+2өДЦөҙуУЪ·ҙұИАэәҜКэy=![]() өДЦөxөДИЎЦө·¶О§Ј®
өДЦөxөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ2017ДкИ«Зті¬ј¶јЖЛг»ъ500ЗҝГыөҘ№«ІјЈ¬ЦР№ъі¬ј¶јЖЛг»ъЎ°ЙсНюЎӨМ«әюЦ®№вЎұәНЎ°МмәУ¶юәЕЎұРҜКЦ¶бөГЗ°БҪГыЈ®ТСЦӘЎ°ЙсНюЎӨМ«әюЦ®№вЎұөДёЎөгФЛЛгЛЩ¶ИКЗЎ°МмәУ¶юәЕЎұөД2.74ұ¶Ј®ХвБҪЦЦі¬ј¶јЖЛг»ъ·ЦұрҪшРР100ТЪТЪҙОёЎөгФЛЛгЈ¬Ў°ЙсНюЎӨМ«әюЦ®№вЎұөДФЛЛгКұјдұИЎ°МмәУ¶юәЕЎұЙЩ18.75ГлЈ¬ЗуХвБҪЦЦі¬ј¶јЖЛг»ъөДёЎөгФЛЛгЛЩ¶ИЈ®ЙиЎ°МмәУ¶юәЕЎұөДёЎөгФЛЛгЛЩ¶ИОӘ![]() ТЪТЪҙО/ГлЈ¬ТАМвТвЈ¬ҝЙБР·ҪіМОӘ___________Ј®
ТЪТЪҙО/ГлЈ¬ТАМвТвЈ¬ҝЙБР·ҪіМОӘ___________Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэЦбЙПЈ¬өгOОӘФӯөгЈ¬өгAұнКҫөДКэОӘ10Ј¬¶ҜөгBЎўCФЪКэЦбЙПТЖ¶ҜЈ¬ЗТЧЬұЈіЦBCЈҪ3ЈЁөгCФЪөгBУТІаЈ©Ј¬ЙиөгBұнКҫөДКэОӘmЈ®
![]()
ЈЁ1Ј©ИзНј1Ј¬ИфBОӘOAЦРөгЈ¬ФтACЈҪЎЎ ЎЎЈ¬өгCұнКҫөДКэКЗЎЎ ЎЎЈ»
ЈЁ2Ј©ИфBЎўC¶јФЪПЯ¶ОOAЙПЈ¬ЗТACЈҪ2OBЈ¬ЗуҙЛКұmөДЦөЈ»
ЈЁ3Ј©өұПЯ¶ОBCСШЙдПЯAO·ҪПтТЖ¶ҜКұЈ¬ИфҙжФЪAC©ҒOBЈҪ![]() ABЈ¬ЗуВъЧгМхјюөДmЦөЈ®
ABЈ¬ЗуВъЧгМхјюөДmЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
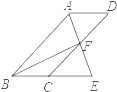
ЎҫМвДҝЎҝИзНјЈ¬ЛДұЯРОABCDОӘЖҪРРЛДұЯРОЈ¬ЎПBADөДҪЗЖҪ·ЦПЯAEҪ»CDУЪөгFЈ¬Ҫ»BCөДСУіӨПЯУЪөгEЈ®
ЈЁ1Ј©ЗуЦӨЈәBE=CDЈ»
ЈЁ2Ј©Б¬ҪУBFЈ¬ИфBFЎНAEЈ¬ЎПBEA=60ЎгЈ¬AB=4Ј¬ЗуЖҪРРЛДұЯРОABCDөДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј1Ј¬ФЪХэ·ҪРОABCDЦРЈ¬PОӘ¶ФҪЗПЯBDЙПөДТ»өгЈ¬өгEФЪADөДСУіӨПЯЙПЈ¬ЗТPAЈҪPEЈ¬PEҪ»CDУЪFЈ¬Б¬ҪУCEЈ®
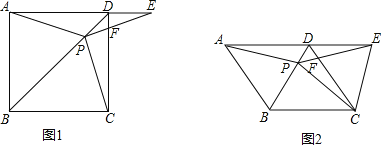
ЈЁ1Ј©ЗуЦӨЈәЎчPCEКЗөИСьЦұҪЗИэҪЗРОЈ»
ЈЁ2Ј©ИзНј2Ј¬°СХэ·ҪРОABCDёДОӘБвРОABCDЈ¬ЖдЛыМхјюІ»ұдЈ¬өұЎПABCЈҪ120ЎгКұЈ¬ЕР¶ПЎчPCEөДРОЧҙЈ¬ІўЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҝОМвРЎЧйҙУДіКР2000ГыҫЕДкј¶ДРЙъЦРЈ¬Лж»ъійИЎБЛ1000ГыҪшРР50ГЧЕЬІвКФЈ¬ІўёщҫЭІвКФҪб№ыЦЖіЙБЛИзПВөДНіјЖұнЈ®
өИј¶ | ИЛКэ | °Щ·ЦұИ |
УЕРг | 200 | 20% |
БјәГ | 600 | 60% |
ј°ёс | 150 | 15% |
І»ј°ёс | 50 |
|
ЈЁ1Ј©![]() өДЦөОӘ______Ј»
өДЦөОӘ______Ј»
ЈЁ2Ј©ЗлҙУұнёсЦРИОТвСЎИЎТ»БРКэҫЭЈ¬»жЦЖәПАнөДНіјЖНјАҙұнКҫЈ»ЈЁ»жЦЖТ»ЦЦјҙҝЙЈ©
ЈЁ3Ј©№АјЖХв20000ГыҫЕДкј¶ДРЙъЦР50ГЧЕЬҙпөҪБјәГәНУЕРгөИј¶өДЧЬИЛКэЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ°ҙТӘЗуҪвІ»өИКҪЈЁЧйЈ©
ЈЁ1Ј©ЗуІ»өИКҪ![]() өД·ЗёәХыКэҪвЈ®
өД·ЗёәХыКэҪвЈ®
ЈЁ2Ј©ҪвІ»өИКҪЧй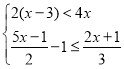 Ј¬Іў°СЛьөДҪвјҜФЪКэЦбЙПұнКҫіцАҙЈ®
Ј¬Іў°СЛьөДҪвјҜФЪКэЦбЙПұнКҫіцАҙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈәИзНјЈ¬ФЪЎчABCЦРЈ¬AB=AC,AEКЗҪЗЖҪ·ЦПЯЈ¬BMЖҪ·ЦЎПABCҪ»AEУЪөгM,ҫӯ№эB,MБҪөгөДЎСOҪ»BCУЪөгG,Ҫ»ABУЪөгF,FBЗЎОӘЎСOөДЦұҫ¶.

ЈЁ1Ј©ЗуЦӨЈәAEУлЎСOПаЗРЈ»
ЈЁ2Ј©өұBC=4,cosC=![]() КұЈ¬ЗуЎСOөД°лҫ¶.
КұЈ¬ЗуЎСOөД°лҫ¶.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com