
����Ŀ����I��Բ���������________��
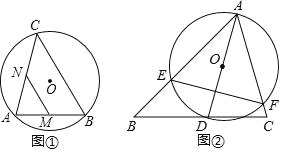
������ͼ�٣�AB �ǡ�O ������AB=8���� C �ǡ�O �ϵ�һ������������ACB=45�㣬 ���� M��N �ֱ��� AB��AC ���е㣬�� MN ���ȵ����ֵ��___��
������ͼ�ڣ���ABC �У���BAC=60�㣬��ABC=45�㣬AB=4��D �DZ� BC �ϵ�һ�����㣬�� AD Ϊֱ������O���ֱ� AB��AC �ڵ� E��F������ EF�����߶� EF ���ȵ���СֵΪ_____��
���𰸡�ֱ�� 4![]()
![]()
��������
������ֱ����Բ������ҽ�ɣ�
��������λ�߶����õ� MN �ij����ʱ��BC ��� BC ���ʱ��ֱ�����Ӷ����ֱ����Ϳ���������ֵ��
�����ɴ��߶ε����ʿ�֪���� AD Ϊ��ABC �ı� BC �ϵĸ�ʱ��ֱ�� AD ��̣� ��ʱ�߶� EF=2EH=20Esin��EOH=20Esin60�㣬��˵��뾶 OE ���ʱ��EF ��̣�����OE��OF���� O ���� OH��EF������Ϊ H���� Rt��ADB �У���ֱ������
![]() ����ֱ�� AD����Բ�ܽǶ�����֪��EOH= ��EOF=��BAC=60�㣬�� Rt��EOH �У�
����ֱ�� AD����Բ�ܽǶ�����֪��EOH= ��EOF=��BAC=60�㣬�� Rt��EOH �У�
��ֱ���������� EH���ɴ���������֪ EF=2EH��
�⣺����ֱ����Բ������ң��ʴ�Ϊ��ֱ����
������ͼ 1���ߵ� M��N �ֱ��� AB��AC ���е㣬
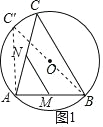
��MN=![]() BC��
BC��
�൱ BC ȡ�����ֵʱ��MN ��ȡ�����ֵ���� BC ��ֱ��ʱ��BC ��� ���� BO ���ӳ�����O �ڵ� C�䣬���� AC�䣬
��BC���ǡ�O ��ֱ����
���BAC��=90�㣮
�ߡ�ACB=45�㣬AB=8��
���AC��B=45�㣬
��BC��= ![]() =
=![]() =8
=8![]() ��
��
��MN ���=4![]() �� �ʴ�Ϊ��4
�� �ʴ�Ϊ��4![]() ��
��
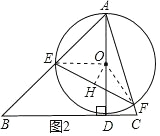
�����ɴ��߶ε����ʿ�֪���� AD Ϊ��ABC �ı� BC �ϵĸ�ʱ��ֱ�� AD ��̣�
��ͼ 2 ��
���� OE��OF���� O ���� OH��EF������Ϊ H��
���� Rt��ADB �У���ABC=45�㣬AB=4��
��AD=BD=2![]() ������ʱԲ��ֱ��Ϊ 2
������ʱԲ��ֱ��Ϊ 2![]() ��
��
��Բ�ܽǶ�����֪��EOH=![]() ��EOF=��BAC=60�㣬
��EOF=��BAC=60�㣬
���� Rt��EOH ��EH=OEsin��EOH=![]() ��
��![]() =
=![]() ��
��
�ɴ���������֪ EF=2EH=![]() �� �ʴ�Ϊ��
�� �ʴ�Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��������C��y��ax2+2x+c�ཻ�ڵ�A(��1��0)�͵�B(2��3)���㣮
(1)��������C��������ʽ��
(2)����M��λ��ֱ��AB�Ϸ��������ϵ�һ���㣬��![]() ��������ʱ�����ʱ
��������ʱ�����ʱ![]() �����S����M�����꣮
�����S����M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB��6��EΪAB���е㣬����ADE��DE���۵õ���FDE���ӳ�EF��BC��G��FH��BC������ΪH������BF��DG.���½��ۣ���BF��ED������DFG�ա�DCG������FHB�ס�EAD����tan��GEB��![]() ����S��BFG��2.6��������ȷ�ĸ�����( )
����S��BFG��2.6��������ȷ�ĸ�����( )
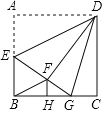
A. 2B. 3C. 4D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ�ƽ�����ƶ������ij�س�̨���������ס�ҽ����ƶ��������������ҵ���֡������йܺ��ذ�Ǩ�����ְ����ʩ��ÿ��ƶ������������2��5�ְ����ʩ���ְ�������2�֡�3�֡�4�ֺ�5�ְ����ʩ��ƶ�����ֱ��ΪA��B��C��D��ƶ������Ϊ��˰����ʩ�Ƿ���ʵ�������ȡ������ƶ�������е��飬�ֽ��ռ������ݻ��Ƴ�����������������ͳ��ͼ��
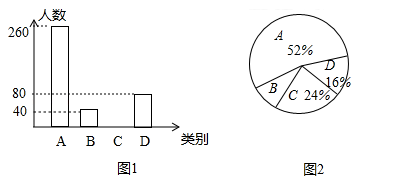
�����ͼ����Ϣ�ش���������⣺
��1�����γ��������˶��ٻ�ƶ������
��2������˶��ٻ�C��ƶ����������ȫͳ��ͼ��
��3�����õع���13000��ƶ��������������ٵõ�4������ʩ�Ĵ�Լ�ж��ٻ���
��4��Ϊ���õ����þ���ƶ������������D��ƶ�����еļס��ҡ��������Ļ������ѡȡ���������ص�����������״ͼ���б������ǡ��ѡ�мͶ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ���㣨0��1�����Գ���Ϊֱ��x=��1�����н��ۣ���a+b+c��0����a��b+c��1����abc��0����4a��2b+c��0����c��a��1�����У���ȷ���۵ĸ���Ϊ��������
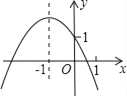
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�dz�Ϊ10m����б��Ϊ30����Զ����ݣ�ƽ̨BD���¥CE��ֱ���������AB�ij�����ȣ���B����ô�¥����C������Ϊ65�㣬���¥CE�ĸ߶ȣ�������������������ο����ݣ�sin65�㣽0.90��tan65�㣽2.14��
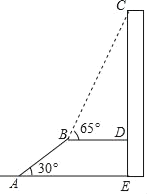
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����AΪ��ǣ�CDΪAB���ϵĸߣ���OΪ��ACD������ԲԲ�ģ����AOB=____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��1��a���Ƿ���������![]() ��ͼ����һ����ֱ��
��ͼ����һ����ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ��Ľ���Ϊ��B��D����B��3����1��������
��ͼ��Ľ���Ϊ��B��D����B��3����1��������
��1�����������Ľ���ʽ��
��2�����D��������ֱ��д��y1��y2ʱx��ȡֵ��Χ��
��3������P��x��0����x������������˶������߶�PA���߶�PB֮��ﵽ���ʱ�����P��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2�����������������У�ÿ��С�����εı߳���1����λ���ȣ���
��1��������ABC�Ƶ�A˳ʱ�뷽����ת90����õ�����A1B1C1����ֱ��д��C1������ꣻ
��2��������ABC����ԭ��O�����ĶԳƵ���A2B2C2����ֱ��д��B2�����꣮
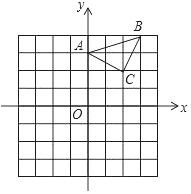
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com