
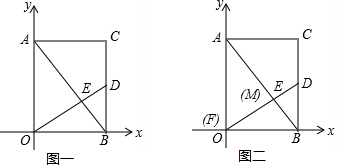
分析 (1)根据△BOD∽△OAB,列出比例式$\frac{BD}{OB}$=$\frac{OB}{AO}$,求得BD的长即可得出点D的坐标;
(2)①分两种情况讨论:当MF⊥AO时,△MFO∽△AOB;当FM⊥OD时,△FOM∽△ABO,分别根据相似三角形的对应边成比例,列出方程式求解即可;
②过点M作MG⊥AO于G,根据△MOG∽△ABO,求得MG=$\frac{96}{25}-\frac{4}{5}t$,再根据S△OMF:S△ABC=9:100,列出关于t的方程式,求得t的值并进行检验即可.
解答 解:(1)∵在矩形AOBC中,OA=8,OB=6,AB⊥OD,
∴∠OBD=∠AOB=90°,∠BOD=∠OAB,AB=10,
∴△BOD∽△OAB,
∴$\frac{BD}{OB}$=$\frac{OB}{AO}$,即$\frac{BD}{6}$=$\frac{6}{8}$,
∴BD=4.5,
∴D(6,4.5);
(2)①由题可得OF=t,EM=t,
Rt△AOB中,OE=$\frac{6×8}{10}$=$\frac{24}{5}$,
如图所示,当MF⊥AO时,△MFO∽△AOB,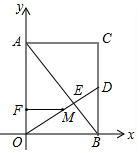
此时,$\frac{OF}{BO}$=$\frac{OM}{BA}$,
即$\frac{t}{6}$=$\frac{\frac{24}{5}-t}{10}$,
解得t=1.8;
如图所示,当FM⊥OD时,△FOM∽△ABO,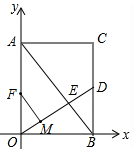
此时,$\frac{OF}{AB}$=$\frac{OM}{BO}$,
即$\frac{t}{10}$=$\frac{\frac{24}{5}-t}{6}$,
解得t=3;
综上所述,当t为1.8秒或3秒时,△MOF与△AOB相似;
②如图所示,过点M作MG⊥AO于G,则∠OGM=∠BOA,∠GOM=∠OBA,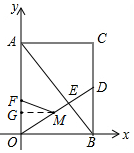
∴△MOG∽△ABO,
∴$\frac{MG}{MO}$=$\frac{AO}{AB}$,即$\frac{MG}{\frac{24}{5}-t}$=$\frac{8}{10}$,
解得MG=$\frac{96}{25}-\frac{4}{5}t$,
∵S△OMF:S△ABC=9:100,
∴$\frac{\frac{1}{2}×OF×MG}{\frac{1}{2}×AC×BC}$=$\frac{9}{100}$,即$\frac{t×(\frac{96}{25}-\frac{4}{5}t)}{6×8}$=$\frac{9}{100}$,
解得t1=3,t2=1.8,
∵FA>3ME,
∴8-t>3t,
解得t<2,
∴t2=1.8符合题意,
∴存在当t=1.8时,S△OMF:S△ABC=9:100.
点评 本题主要考查了相似三角形的判定与性质的综合应用,解题时注意分类讨论思想的运用,解决问题的关键是作辅助线构造相似三角形,利用相似三角形的对应边成比例列出关系式进行计算.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com