
【题目】一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?
(1)设江水的流速为![]() 千米/时,填空:轮船顺流航行速度为_________千米/时,逆流航行速度为_________千米/时,顺流航行100千米所用时间为_________小时,逆流航行60千米所用时间为_________小时.
千米/时,填空:轮船顺流航行速度为_________千米/时,逆流航行速度为_________千米/时,顺流航行100千米所用时间为_________小时,逆流航行60千米所用时间为_________小时.
(2)列出方程,并求出问题的解.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)江水的流速为5千米/时.
;(2)江水的流速为5千米/时.
【解析】
(1)根据轮船顺流航行速度=轮船在静水中的最大航速+江水的流速,逆流航行速度=轮船在静水中的最大航速-江水的流速,即可得到答案;
(2)根据沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,列出方程,即可求解.
(1)∵轮船顺流航行速度=轮船在静水中的最大航速+江水的流速,
∴轮船顺流航行速度为![]() 千米/时,
千米/时,
∵逆流航行速度=轮船在静水中的最大航速-江水的流速,
∴逆流航行速度为![]() 千米/时,
千米/时,
∴顺流航行100千米所用时间为![]() 小时,逆流航行60千米所用时间为
小时,逆流航行60千米所用时间为![]() 小时.
小时.
故答案是:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)根据题意,列方程得:![]() ,
,
方程两边同乘![]() ,得
,得![]() ,
,
解得:![]() .
.
经检验,![]() 是原分式方程的解,且符合题意.
是原分式方程的解,且符合题意.
答:江水的流速为5千米/时.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() 。
。

(1)求点![]() 到
到![]() 轴的距离;
轴的距离;
(2)连接![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,猜想线段![]() 和线段
和线段![]() 的数量关系,并说明理由。
的数量关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学试验(用纸签D、E、F表示)中各抽取一个实验操作进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习等边三角形时发现了直角三角形的一个性质:直角三角形中,![]() 角所对的直角边等于斜边的一半。小明同学对以上结论作了进一步探究.如图1,在
角所对的直角边等于斜边的一半。小明同学对以上结论作了进一步探究.如图1,在![]() 中,
中,![]() ,则:
,则:![]() .
.
探究结论:(1)如图1,![]() 是
是![]() 边上的中线,易得结论:
边上的中线,易得结论:![]() 为________三角形.
为________三角形.
(2)如图2,在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是边
是边![]() 上任意一点,连接
上任意一点,连接![]() ,在
,在![]() 边上方作等边
边上方作等边![]() ,连接
,连接![]() .试探究线段
.试探究线段![]() 与
与![]() 之间的数量关系,写出你的猜想加以证明.
之间的数量关系,写出你的猜想加以证明.
拓展应用:如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上的一动点,以
轴正半轴上的一动点,以![]() 为边作等边
为边作等边![]() ,当点
,当点![]() 在第一象内,且
在第一象内,且![]() 时,求点
时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1, 将Cl绕点B中心对称变换得C2, C2与x轴交于另一点C,将C2绕点C中心对称变换得C3, 连接C与C3的顶点,则图中阴影部分的面积为( )
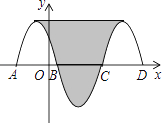
A. 32 B. 24 C. 36 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()
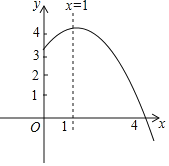
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
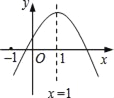
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com