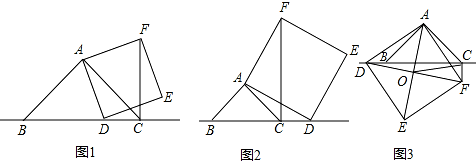
(1)证明:∵四边形ADEF为正方形,
∴AD=AF,∠DAF=90°,
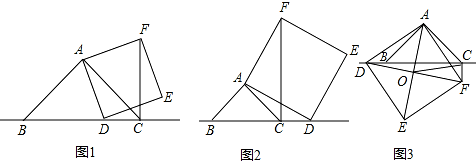
∵∠BAC=90°,
∴∠BAD+∠DAC=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
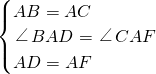
,
∴△ABD≌△ACF(SAS),
∴BD=CF,
∴CF=BC-CD;
(2)解:(1)中结论不成立,图2中的关系式为:CF=BC+CD.理由如下:
∵四边形ADEF为正方形,
∴AD=AF,∠DAF=90°
∵∠BAC=90°,
∴∠BAC+∠DAC=∠DAF+∠DAC,
即∠BAD=∠CAF,
在△ABD和△ACF中,
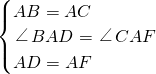
,
∴△ABD≌△ACF(SAS),
∴BD=CF,
∴CF=BC+CD;
图3中的关系式为:CF=CD-BC.理由如下:
∵四边形ADEF为正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=90°,
∴∠DAF-∠BAC=∠BAC-∠BAF,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(SAS),
∴BD=CF,
∴CF=CD-BC.
分析:(1)根据正方形的性质得AD=AF,∠DAF=90°,而∠BAC=90°,根据等角的余角相等得∠BAD=∠CAF,则根据“SAS”可判断△ABD≌△ACF,得到BD=CF,所以CF=BC-CD;
(2)对于图2,由四边形ADEF为正方形得到AD=AF,∠DAF=90°,则∠BAC+∠DAC=∠DAF+∠DAC,即∠BAD=∠CAF,则根据“SAS”可判断△ABD≌△ACF,得到BD=CF,所以CF=BC+CD;
对于图3,由四边形ADEF为正方形得到AD=AF,∠DAF=90°,根据等角的余角相等得∠BAD=∠CAF,则根据“SAS”可判断△ABD≌△ACF,得到BD=CF,所以CF=CD-BC.
点评:本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”.也考查了正方形的性质.


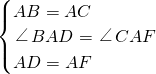 ,
,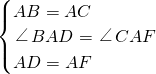 ,
,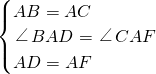 ,
,

 (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.