

分析 (1)找出5表示的点与-3表示的点组成线段的中点表示数,然后结合数轴即可求得答案;
(2)先找出a表示的点与b表示的点所组成线段的中点,从而可求得答案;
(3)先求出每两条相邻折痕的距离,进一步得到最左端的折痕和最右端的折痕与数轴的交点表示的数,即可求得答案.
解答 解:(1)(-3+1)÷2
=-2÷2
=-1.
故折痕与数轴的交点表示的数为-1;
(2)折痕与数轴的交点表示的数为$\frac{a+b}{2}$(用含a,b的代数式表示);
(3)∵对折n次后,每两条相邻折痕的距离为$\frac{5-(-3)}{{2}^{n}}$=$\frac{8}{{2}^{n}}$,
∴最左端的折痕与数轴的交点表示的数是-3+$\frac{8}{{2}^{n}}$,最右端的折痕与数轴的交点表示的数是5-$\frac{8}{{2}^{n}}$.
故答案为:-1;$\frac{a+b}{2}$.
点评 本题主要考查的是数轴的认识,找出对称中心是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
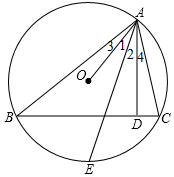 △ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).
△ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com