

 ,
,

科目:初中数学 来源:中华题王 数学 八年级上 (人教版) 人教版 题型:059
(如图所示)取一张矩形的纸进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图(1);第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为![]() ,得Rt△
,得Rt△![]() ,如图(2);第三步:沿
,如图(2);第三步:沿![]() 线折叠得折痕EF,如图(3).利用展开图(4)探究:
线折叠得折痕EF,如图(3).利用展开图(4)探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州翠苑中学九年级上学期10月质量检测数学试卷(解析版) 题型:解答题
如图,矩形ABCD为一本书,AB=12π,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为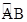 ,最后一张纸CD对应为
,最后一张纸CD对应为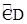 (
(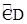 为半圆),
为半圆),
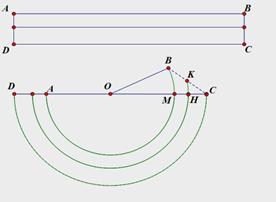
(1)连结OB,求钝角∠AOB= ;
(2)如果该书共有100张纸,求第40张纸对应的弧超出半圆部分的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
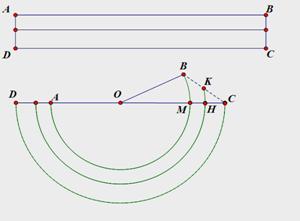
如图,矩形ABCD为一本书,AB=12π![]() ,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为弧AB,最后一张纸CD对应为弧CD(CD为半圆),
,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为弧AB,最后一张纸CD对应为弧CD(CD为半圆),
(1)、连结OB,求钝角∠AOB
(2)、如果该书共有100张纸,求第40张纸对应的弧超出半圆部分的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
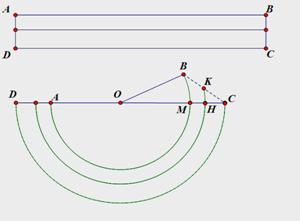
如图,矩形ABCD为一本书,AB=12π,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为![]() ,最后一张纸CD对应为
,最后一张纸CD对应为![]() (
(![]() 为半圆),(1)、连结OB,求钝角∠AOB= ;
为半圆),(1)、连结OB,求钝角∠AOB= ;
(2)、如果该书共有100张纸,求第40张纸对应的弧超出半圆部分的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
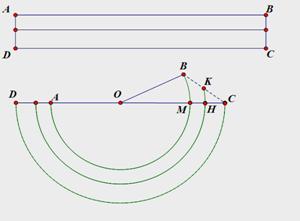
如图,矩形ABCD为一本书,AB=12π![]() ,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为弧AB,最后一张纸CD对应为弧CD(CD为半圆),
,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为弧AB,最后一张纸CD对应为弧CD(CD为半圆),
(1)、连结OB,求钝角∠AOB
(2)、如果该书共有100张纸,求第40张纸对应的弧超出半圆部分的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com