
【题目】如图,AB是⊙O的直径,C为⊙O 上一点,过点C作⊙O的切线DE,AD⊥DE于点D,DE与AB的延长线交于点E,连接AC.

(1)求证:AC平分∠DAE;
(2)若⊙O的半径为2,∠CAB=35°,求![]() 的长.
的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】天猫商城某网店销售童装,在春节即将将来临之际,开展了市场调查发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件;如果每件童装降价1元,那么平均每天可售出2件.
(1)假设每件童装降价![]() 元时,每天可销售 件,每件盈利 元;(用含
元时,每天可销售 件,每件盈利 元;(用含![]() 人代数式表示)
人代数式表示)
(2)每件童装降价多少元时,平均每天盈利最多?每天最多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+3与x轴交于A,B两点,与y轴交于点C,其中点A(-1,0).过点A作直线y=x+c与抛物线交于点D,动点P在直线y=x+c上,从点A出发,以每秒![]() 个单位长度的速度向点D运动,过点P作直线PQ∥y轴,与抛物线交于点Q,设运动时间为t(s).
个单位长度的速度向点D运动,过点P作直线PQ∥y轴,与抛物线交于点Q,设运动时间为t(s).
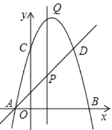
(1)直接写出b,c的值及点D的坐标;
(2)点 E是抛物线上一动点,且位于第四象限,当△CBE的面积为6时,求出点E 的坐标;
(3)在线段PQ最长的条件下,点M在直线PQ上运动,点N在x轴上运动,当以点D、M、N为顶点的三角形为等腰直角三角形时,请求出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
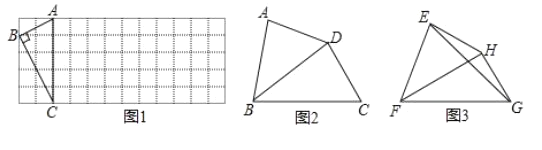
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点 D,使四边形ABCD是以AC为“相似对角线”的四边形(画出1个即可);
(2)如图2,在四边形ABCD中,![]() ,对角线BD平分∠ABC.
,对角线BD平分∠ABC.
求证: BD是四边形ABCD的“相似对角线”;
运用:
(3)如图3,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=![]() .连接EG,若△EFG的面积为
.连接EG,若△EFG的面积为![]() ,求FH的长.
,求FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在一节数学活动课上,老师带领同学们借助几何画板对以下题目进行了研究.如图1,
MN是过点A的直线,点C为直线MN外一点,连接AC,作∠ACD=60°,使AC=DC,在MN上取一点B,使∠DBN=60°.
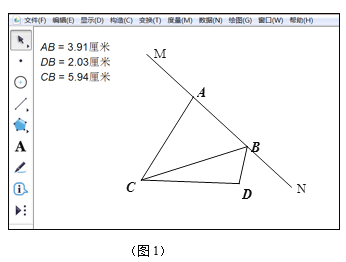
观察发现
(1)根据图1中的数据,猜想线段AB、DB、CB之间满足的数量关系是 ;
(2)希望小组认真思考后提出一种证明方法:将CB所在的直线以点C为旋转中心,逆时针旋转60°,与直线MN交于点E,即可证明(1)中的结论. 请你在图1中作出线段CE,并根据此方法写出证明过程;
实践探究
(3)奋进小组在继续探究的过程中,将点C绕点A逆时针旋转,他们发现当旋转到图2和图3的位置时,∠DBN=120°,线段AB、BD、CB的大小发生了变化,但是仍然满足一定的数量关系,请你直接写出这两种关系:
在图2中,线段AB、DB、CB之间满足的数量关系是 ;
在图3中,线段AB、DB、CB之间满足的数量关系是 ;
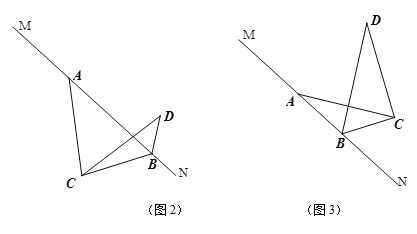
提出问题
(4)智慧小组提出一个问题:若图3中BC⊥CD于点C时,BC=2,则AC为多长?请你解答此问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆八中建校80周年,在体育、艺术、科技等方面各具特色,其中排球选修课是体育特色项目之一.体育组老师为了了解初一年级学生的训练情况,随机抽取了初一年级部分学生进行1分钟垫球测试,并将这些学生的测试成绩(即1分钟的垫球个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级(不包括90),90~120范围内的记为C级(不包括120),120~150范围内的记为B级(不包括150),150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:

(1)在这次测试中,一共抽取了 名学生,并补全频数分布直方图:在扇形统计图中,D级对应的圆心角的度数为 度.
(2)王攀同学在这次测试中1分钟垫球140个.他为了了解自己垫球个数在年级排名的大致情况,他把成绩为B等的全部同学1分钟垫球人数做了统计,其统计结果如表:
成绩(个) | 120 | 125 | 130 | 135 | 140 | 145 |
人数(频数) | 2 | 8 | 3 | 10 | 9 | 8 |
(垫球个数计数原则:120<垫球个数≤125记为125,125<垫球个数≤130记为130,依此类推)请你估计王攀同学的1分钟垫球个数在年级排名的大致情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
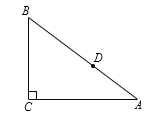
【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com