
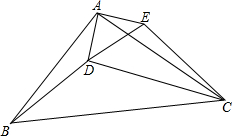
 如图,△ABC中,AB=AC,点D在△ABC内部,以AD为腰作等腰△ADE,AD=AE,且∠BAC=∠DAE=100°,∠BDC=140°,∠BDA=α,连接BD、CD,当α=130°时,试判断△CDE的形状,并说明理由.
如图,△ABC中,AB=AC,点D在△ABC内部,以AD为腰作等腰△ADE,AD=AE,且∠BAC=∠DAE=100°,∠BDC=140°,∠BDA=α,连接BD、CD,当α=130°时,试判断△CDE的形状,并说明理由. 分析 结论:△CDE是直角三角形.只要证明△BAD≌△CAE,推出∠BDA=∠AEC=130°,由AD=AE,∠DAE=100°,推出∠AED=∠ADE=40°,求出∠DEC即可解决问题.
解答 解:结论:△CDE是直角三角形.
理由: ∵∠BAC=∠DAE=100°,
∵∠BAC=∠DAE=100°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{BA=CA}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE,
∴∠BDA=∠AEC=130°,
∵AD=AE,∠DAE=100°,
∴∠AED=∠ADE=40°,
∴∠DEC=∠AEC-∠AED=130°-40°=90°,
∴△DEC是直角三角形.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是正确寻找全等三角形,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
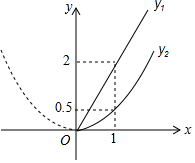 随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)
随着成都市近几年城市建设的快速发展,对花木的需求量逐年提高,某园林专业户计划投资种植树木及花卉,根据市场调查与预测,种植树木的利润y1与投入资金x成正比例函数关系;种植花卉的利润y2与投入资金x成二次函数关系,如图所示(利润与投入资金的单位:万元)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-(x-1)2-2 | B. | y=-(x-1)2+2 | C. | y=-(x-1)2+4 | D. | y=-(x+1)2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任何有理数均可用分数形式表示 | |
| B. | 数轴上的点与有理数一一对应 | |
| C. | 1和2之间的无理数只有<“m“:math xmlns:dsi='http://www.dessci.com/uri/2003/MathML'dsi:zoomscale='150'dsi:_mathzoomed='1'style='CURSOR:pointer; DISPLAY:inline-block'>2$\sqrt{2}$ | |
| D. | 无限小数是无理数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com